0.1 décibels
Vous analysez le spectre d’un signal sinusoïdal de fréquence 100 Hz, 1 volt crête délivré par un générateur basse fréquence (GBF).
En plaçant le curseur sur le pic à 100 Hz, l’analyseur vous indique un niveau de -3 dB
Question : quelle est la tension de référence pour le calcul des décibels ?
0.2 Fréquence d’échantillonnage et nombre de points par période
On échantillonne un signal sinusoïdal de fréquence F_{sin}=1000 Hz à une fréquence d’échantillonnage fixe F_e=10 kHz pendant une durée d’enregistrement T_{enr}=10 secondes.
Combien enregistre-t-on de points par seconde ?
Quel est l’intervalle de temps \Delta t entre deux échantillons ?
Combien de points N_{pts} a-t-on enregistré au total ?
Combien y-a-t’il de points N_{T} par période du sinus ?
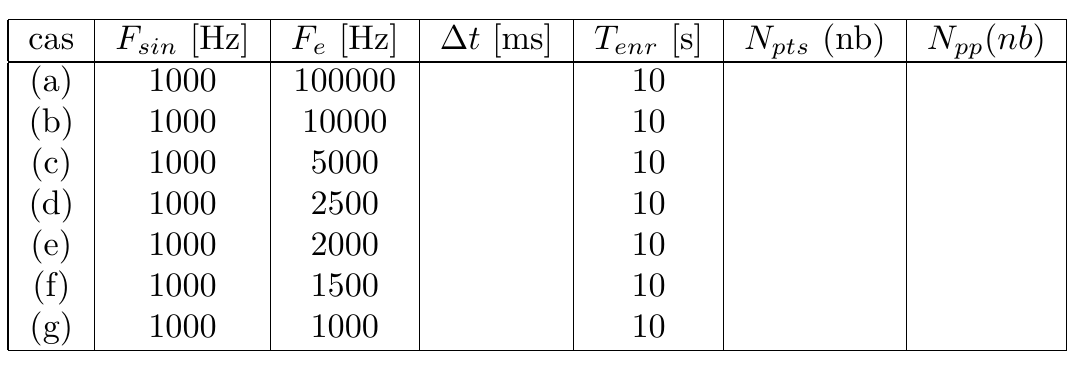
Réprendre les questions 1 à 4 pour des sinusoïdes de fréquences F_{sin} définies dans le tableau ci-dessous:
0.3 Résolution fréquentielle
Sur un logiciel ou appareil d’analyse du signal, on numérise un signal
On fixe le nb de points du spectre à 1000 points (on dit parfois 1000 lignes dans certains logiciels ou appareils)
On enregistre 3 spectres en demandant une analyse sur des bandes de fréquences différentes :
F \in [0, 100] Hz
F \in [0, 1000] Hz
F \in [0, 10000] Hz
Question : Pour chaque spectre, déterminez la résolution fréquentielle \Delta f
0.4 Résolution fréquentielle et analyse
On considère qu’il faut au minimum huit points de séparation pour distinguer deux pics d’ampliude dans le spectre.
Quelle est la résolution nécessaire pour mesurer l’ampltude de 3 pics caractérisant les fréquences de rotation des axes d’une machine à 14.67 Hz, 18.2 Hz, et 23.2 Hz ?
On considère le cas où on effectue 3 analyses sur les gammes de fréquence [0,100] Hz, [0,1000] Hz, [0, 10000] Hz, avec des résolutions respecctives de 0.25, 2.5, et 25 Hz. Qu’allez-vous observer pour ces 3 fréquences ?
0.5 Lien entre les paramètres d’analyse
Les paramètres d’analyse sont généralement liés
Vous avez demandé à un logiciel d’analyser le spectre d’un signal dans la gamme de fréquence [0, 5000] Hz (étendue du spectre)
Le graphique de l’amplitude en fonction du temps vous indique que la résolution temporelle est \Delta t = 78.125 \rm{\mu s}.
Quelle est la fréquence d’échantillonnage F_e ?
Pouvez-vous expliquer la relation entre la fréquence maximum de l’intervalle analysé et la fréquence d’échantillonnage ?
Le graphique de l’amplitude du spectre indique une résolution fréquentielle \Delta f = 12.8 Hz. Sur combien de points l’axe des fréquences est-il discrétisé ?
Vous analysez un signal dont une des fréquences est à 106 Hz.
A quelle fréquence verrez-vous le pic d’amplitude correspondant ?
Combien de points y-a-t’il par période du sinus à 106 Hz ?
La longeur de l’enregistrement est 80 ms. Combien y-a-t’il de points enregistrés ?
Vous modifiez les paramètres d’analyse et réglez l’étendue fréquentielle sur [0 250] Hz.
Sachant que les relations entre les paramètres sont identiques, déterminez les nouvelles valeurs de : la résolution temporelle \Delta t, la fréquence d’échantillonnage F_e, la résolution spectrale \Delta f
A quelle fréquence verrez-vous le pic d’amplitude correspondant à la fréquence 106 Hz ?
Quel sera le nombre de points par période du sinus de fréquence 106 Hz ?
0.6 Représentation spectrale, conversion d’unités
Données
On considère la situation où vous mesurez les vibrations d’une structure et relevez directement l’amplitude de la sortie de l’amplificateur de l’accéléromètre en volts.
On connait la sensibilité en mv/g (avec g = 9.81 \rm{m/s^2}) : S = 10.33 \ \rm{mv}/g
On connaît le gain de l’amplificateur de l’accéléromètre : G_{dB} = 20 dB
Valeurs mesurées :
| F [Hz] | 500 | 565 | 573 | 578 | 586 | 750 | 756 | 765 | 777 | 952 | 956 | 968 | 1075 | 1155 | 1179 | 1192 | 1295 | 1302 | 1304 | 1310 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U [mV] | 192 | 496 | 1390 | 824 | 352 | 680 | 1540 | 776 | 408 | 696 | 1060 | 448 | 40 | 160 | 464 | 280 | 48 | 128 | 192 | 120 |
| \gamma_{rms} [g] | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||
| V_{rms} [mm/s] | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||
| X_{rms} [\mu m] | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
Table : Valeurs mesurées. NB: U est l’amplitude mesurée.
Questions
Pour les 5 valeurs indiquées en gras, calculez :
les valeurs efficaces de l’accélération \gamma_{rms} en g à partir de l’amplitude de la tension électrique, du gain de l’amplificateur, et de la sensibilité
les valeur de la vitesse efficace V_{rms} à partir de l’accélération (indication, il faut intégrer le signal de l’accélération à ces fréquences)
les valeurs du déplacement efficace X_{rms} à partir de la vitesse (indication, il faut intégrer le signal de l’accélération à ces fréquences)
Tracez ces 5 valeurs en fonction de la fréquence Commentez les résultats