10 Analyse Spectrale

Avertissement :

Dans cette page, on se limite à introduire les notions élémentaires pour une prermière approche, en lien avec l’acquisition numérique du signal. L’ambition n’est pas d’être complet et exhaustif.

10.1 Introduction

L’analyse spectrale consiste à analyser le contenu fréquentiel d’un signal.
Pour sensibiliser les principes et l’intérêt de l’analyse des fréquences qui constituent les signaux alternatifs, considérons d’abord le cas du signal ci-dessous, rerprésenté en fonction du temps comme on pourrait le visualiser sur un oscilloscope :
On observe bien 2 sinusoïdes superposées, et l’écoute du signal nous permet également de distinguer deux fréquences bien distinctes
- signal audio :
- On distingue deux composantes :
Remarque : Comme nous percevons mieux les fréquences élevées que les fréquences graves, malgré la différence d’amplitude que l’on peut observe, le signal de fréquence élevée nous appparaît, à l’écoute, à peu près du même niveau que la basse fréquence. Cette sensation déppend aussi du système d’écoute (haut-parleurs, casque) et de l’appareil (ordinateur ou tablette, smartphone).Remarque : Comme nous percevons mieux les fréquences élevées que les fréquences graves, malgré la différence d’amplitude que l’on peut observe, le signal de fréquence élevée nous appparaît, à l’écoute, à peu près du même niveau que la basse fréquence. Cette sensation déppend aussi du système d’écoute (haut-parleurs, casque) et de l’appareil (ordinateur ou tablette, smartphone).
En écoutant le signal et en observant la forme d’onde, c’est à-dire l’amplitude en fonction du temps, nous avons pu dans ce cas simple distinguer deux composantes fréquentielles, et pouvons réduire l’information pour décrire le signal temporel en précisant la fréquence et l’amplitude de ces deux composantes.
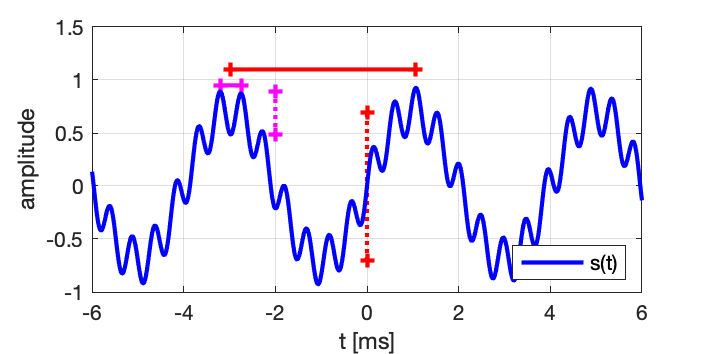
Dans ce cas simple, l’analyse du signal temporel avec des curseurs comme sur un oscilloscope permet d’évaluer approximativement l’amplitude et la période des deux composantes, et en déduire la fréquence :
On en déduit ds valeurs approchées des amplitudes et des fréquences :

\tilde{F_1}=248 Hz (valeur exacte F_1 = 250 Hz) ;
\tilde{F_2}=2205 Hz (valeur exacte F_2 = 2100 Hz) ;
\tilde{A_1}=0.698 (valeur exacte A_1 = 0.708) ;
\tilde{A_2}=0.205 (valeur exacte A_2 = 0.224 ).
On peut alors réduire l’information et représenter le signal sous la forme d’une courbe représentant l’amplitude en fonction de la fréquence :

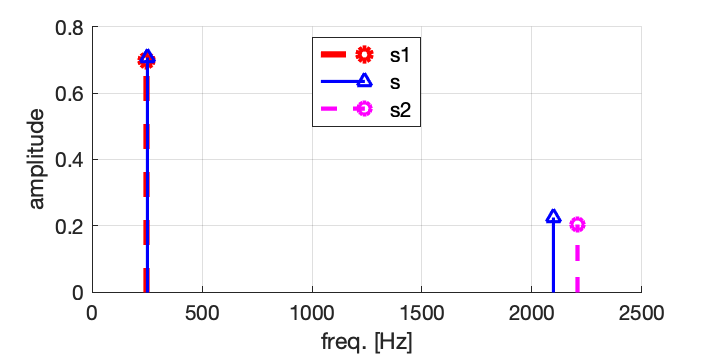
Ce type de représentation, l’amplittude en fonction de la fréquence, est le spectre du signal.
Dans de nombreuses applications, et notamment en aoustique, vibrations, audio, électronique, etc, on représente souvent les amplitudes en échelle logarithmique, et notamment en décibels.

Si on choisit arbitrairement la valeur 1 comme référence, on peut représenter l’amplitude A du signal en \mathrm{dB}_{ref \ 1} en calculant la valeur en décibels 20 \log\left( A / 1 \right) :

Remarque : En pratique, on utilisera des valeurs de références standard pour les dB selon la nature du signal. Par exemple: 1 Volt ou 1 microVolt, efficace, 1 Watt, 20 microPascals, 1 g, 1 \mathrm{m}/\mathrm{s}^2, etc.

L’exemple simple que nous venons de discuter en détails permet de comprendre que l’on peut analyser et représenter un signal en fonction de la fréquence (représentation spectrale, ou simplement spectre) au lieu d’une représentation temporelle (ou forme d’onde).

Mais pour des signaux plus complexes l’analyse ne peut pas se faire aussi simplement et il faut utiliser des outils plus spécifiques. Par exemple, en écoutant le signal ci-dessous, qui contient 5 fréquences superposées, l’analyse est difficile, voire impossible, à partir du signal temporelle, ou même à l’écoute .

10.2 Représentation du spectre d’un signal simple

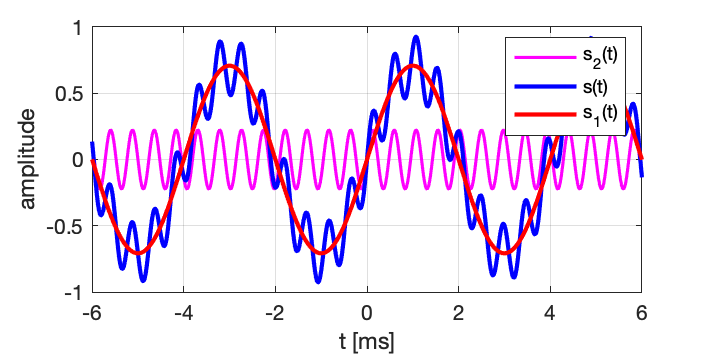
Considérons un signal constitué de la somme de 2 composantes sinusoïdales
- composante 1 : s_1(t) = A_1 \sin (2 \pi F_1 t + \phi_1)
- composante 2: s_2(t) = A_2 \sin (2 \pi F_2 t + \phi_2)
- Somme (ou “Mix” en audio) : s(t) = s_1 (t) + s_2 (t) =A_1 \sin (2 \pi F_1 t + \phi_1) + A_2 \sin (2 \pi F_2 t + \phi_2)

où A_1 et A_2 sont les ampltudes, F_1 et F_2 les fréquences, et \phi_1 et \phi_2 les phases par rapport à une référence commune.

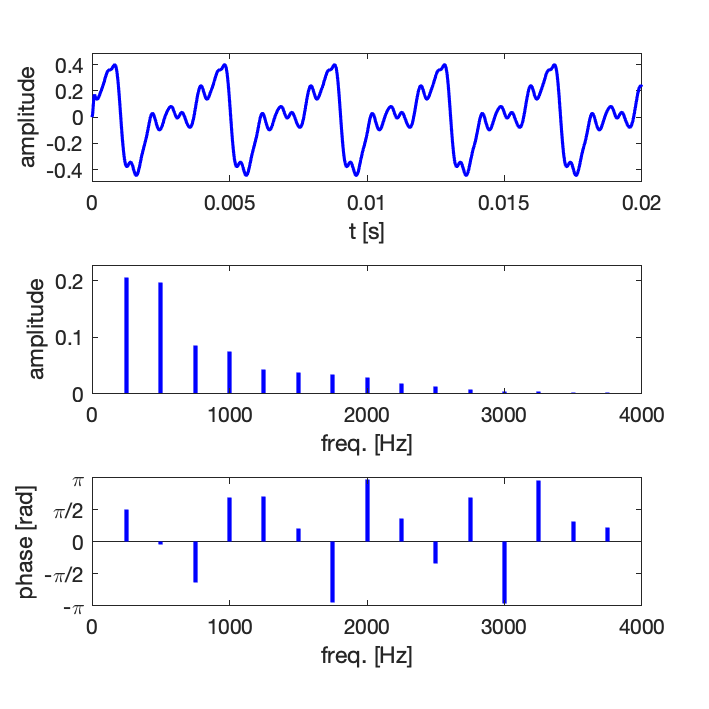
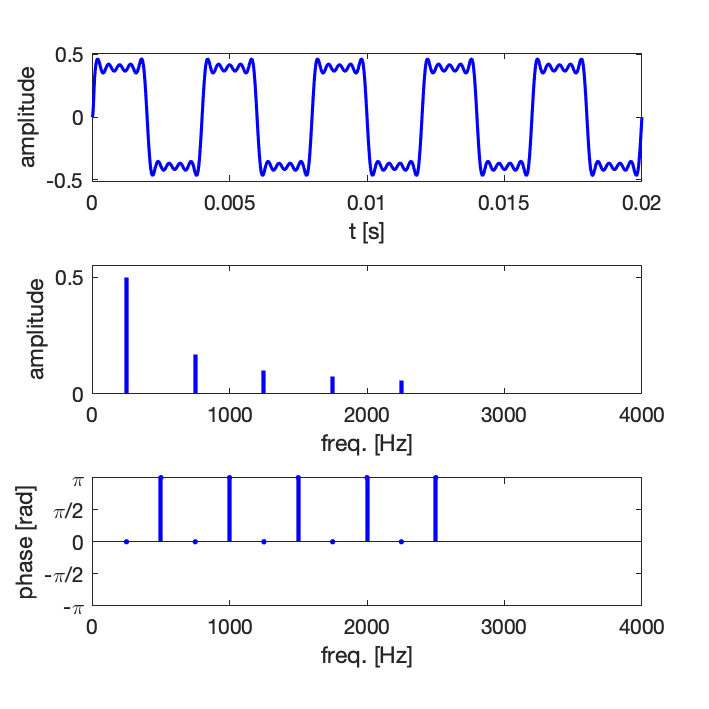
Le signal et ses composantes sont représentées ci-dessous en fonction du temps, ainsi qu’en fonction de la fréquence en traçant l’amplitude et la phase des composantes :
Remarques :
- La phase est parfois un paramètre parfois très important, et parfois non.
- Très souvent on représente uniquement l’amplitude en échelle logarithmique par rapport à une référence, sans préciser la phase.
Important: pour représenter le spectre d’un signal, il faut d’abord savoir l’analyser et extraire les paramètres de chaque composante fréquentielle.
- L’analyse est lorsque l’on cherche à évaluer les amplitudes et éventuellement la phase des différentes composantes fréquentielles
- On parle de synthèse lorsque l’on reconstitue le signal en sommant les différentes composante. (En musique, la synthèse sonore par addition de composantes sinusoïdales est appelée “synthèse additive”)

10.3 Signaux périodiques - séries de Fourier

Les signaux périodiques sont constitués de composantes dites harmoniques, c’est-à-dire telles que les fréquences F_{nh} des différentes composantes du signal ont des fréquences liées à une fréquence fondamentale F_0 de la manière suivante :

F_{nh} = n F_0, \ \ \text{avec} \ \ n= 1, 2, 3, 4, ...

Exemple :

*Exemple de signal périodique (15 composantes harmoniques, fréquence fondamentale 250 Hz)*

Remarque : toutes les composantes n ne sont pas forcément présentes dans le signal, ou, autrement dit, certaines peuvent avoir une amplitude A_n nulle. La fondamentale peut également avoir une amplitude nulle.
L’analyse des fréquences des signaux périodique sera vue en cours de mathématiques dans le cours sur les séries de Fourier.
Remarque : l’analyse spectrale est aussi appelée analyse de Fourier en référence au Mathématicien et Physicien Joseph Fourier wikipedia
Sans développer un cours de mathématiques ici, on présente ci-dessous quelques élément sur la décomposition en séries de Fourier

10.3.1 Décomposition en fonctions sinus et cosinus :

Avertissements :
- il ne s’agit pas ici d’être complet, mais de présenter quelques notions de base avant de consulter un cours dédié aux séries de Fourier
- On se place dans un contexte d’analyse de signaux réels, issus par exemple de capteurs et d’appareils de mesure.
On aborde souvent la décomposition de signaux périodiques s(t) sous la forme de séries du type

S_n (t) = a_0 + \sum_{n=0}^{n=N} a_n \sin(n \omega_0 t) + \sum_{n=0}^{n=N} b_n \sin(n \omega_0 t) où :
- n = 1, 2, 3..., a_0, a_n, et b_n sont des coefficients réels;
- \omega_0, f_0 = \omega_0 / (2 \pi), et T_0 = 2 \pi / \omega sont la pulsation, la fréquence, et la période fondamentales.
On peut écrire la série en faisant apparaître l’argument des fonctions sinus ou cosinus sous différentes formes : (n \omega_0 t) ou ( 2 \pi n f_0 t), ou encore (n 2 \pi t / T_0 ). On trouve aussi des formes où l’on fait apparaître \omega_n = n \omega_0, f_n = n f_0.
Les coefficients a_0, a_n, et b_n se déterminent comme ceci :
- le coefficient a_0 correspond à la composante ontinue du signal (sa moyenne sur une période) :
a_0 = \frac{1}{T_0} \int_0^{T_0} s(t) \mathrm{d}t

Les autres coefficients euvent être vus comme une projection sur une base de fonctions, de manière similaire à la décomposition de vecteurs en composantes selon des vecteurs de base.
- coefficients a_n, avec n\geq 1, et f_n = n \ f_0 :
a_n = \frac{1}{T_0} \int_0^{T_0} s(t) \sin(2 \pi f_n \ t)\mathrm{d}t
- coefficients b_n, avec n\geq 1, et f_n = n \ f_0 :
b_n = \frac{1}{T_0} \int_0^{T_0} s(t) \cos(2 \pi f_n \ t)\mathrm{d}t
Remarque importante : Le nombre N de composantes harmoniques à prendre en compte dépend du signal. Ce nombre eut être fini, ou infini. Lorsque le nombre de composantes n’est pas suffisant, le signal S_n(t) diffère du signal original s(t).

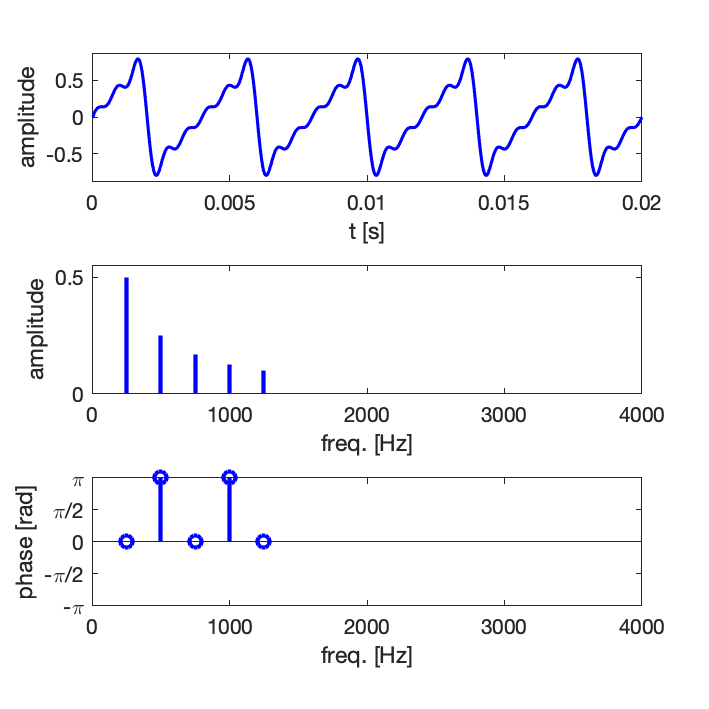
Exemple 1 : synthèse d’un signal de forme dent de scie avec un nombre croissant de composantes harmoniques : 5, 10, 15

Comme en pratique la série ne peut pas être infinie, on observe des oscillations résiduelles, il s’agit du phénomène de Gibbs [en savoir plus sur Wikipedia].

*Synthèse par série de Fourier d’un signal triangle, 5 premiers harmoniques*

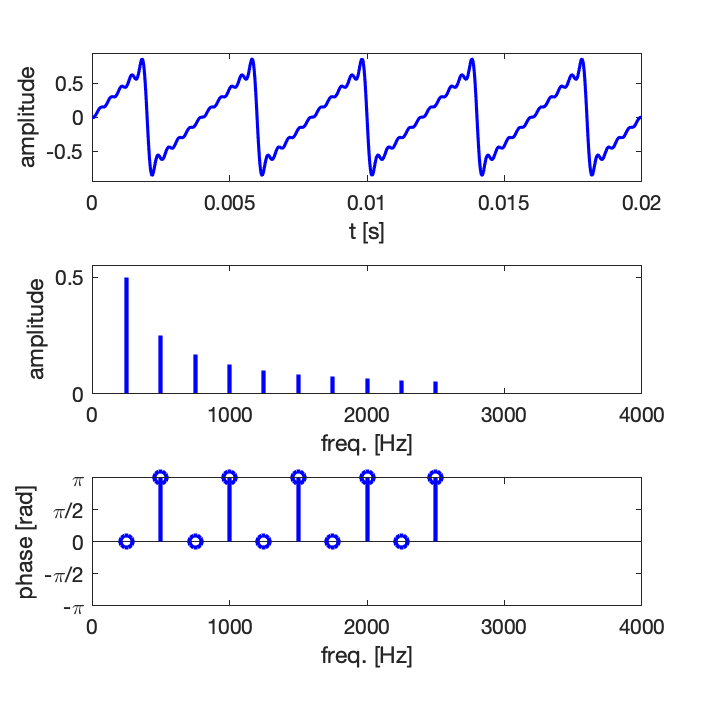
*Synthèse par série de Fourier d’un signal triangle, 10 premiers harmoniques*

*Synthèse par série de Fourier d’un signal triangle, 15 premiers harmoniques*

Exemple 2 : synthèse d’un signal de forme dent de scie avec un nombre croissant de composantes harmoniques : 5, 10, 15

Comme en pratique la série ne peut pas être infinie, on observe des oscillations résiduelles, il s’agit du phénomène de Gibbs [en savoir plus sur Wikipedia].

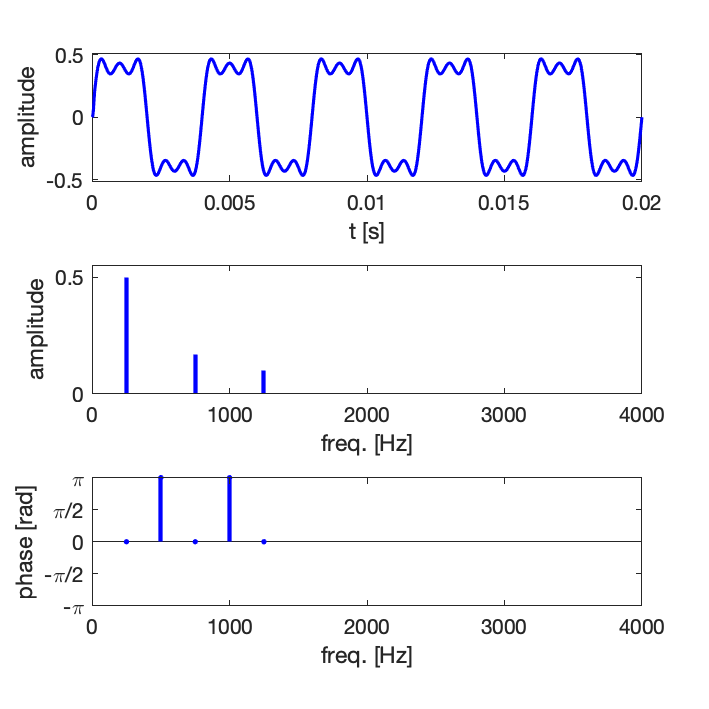
*Synthèse par série de Fourier d’un signal carré, 5 premiers harmoniques (en vrai, seuls les harmoniques impairs sont non nuls, donc les composantes à f_1, f_3, f_5).*

*Synthèse par série de Fourier d’un signal triangle, 10 premiers harmoniques (non nuls : 1, 3, 5, 7, 9)$)*

*Synthèse par série de Fourier d’un signal triangle, 15 premiers harmoniques (non nuls : 1, 3, 5, 7, 9, 11, 13, 15)*

10.3.2 Décomposition en fonctions sinus ou cosinus

On peut aussi écrire la décomposition en série de Fourier de la manière suivante :

S_n (t) = a_0 + \sum_{n=0}^{n=N} A_n \sin(2 \pi f_n \ t + \phi_n)

ou encore

S_n (t) = a_0 + \sum_{n=0}^{n=N} A_n \cos(2 \pi f_n \ t + \psi_n)

avec f_n = n \ f_0

10.3.3 Décomposition en fonctions exponentielles complexes

Les fonctions sinus et cosinus pouvant être décomposées en exponentielles, on peut aussi écrire les séries de Fourier en utilisant les fonctions exponentielles complexes :

\displaystyle S_n = \sum _{n=-\infty }^{+\infty }c_{n}{\rm {e}}^{{\rm {j}}2 \pi f_n \ t}

avec f_n = n \ f_0 (remarque : pour n=0, on retrouve a_0)

Remarque : en électricité et en physique, pour éviter la confusion avec le symbole du courant élecctrique, on préfère souvent nommer le nombre complexe \sqrt{-1} en utilisant la lettre j au lieu de la lettre i, qui est préférée en mathématiques.
En savoir plus sur wikipedia

(NB: les notations et l’ordre des explication, plus complètes et plus rigoureuses, peuvent parfois différer des choix faits ici, où l’on se contente d’une première appproche, et avec un point de vue “pratique”, notamment en privilégiant le cas des signaux réel.)

10.4 Généralisation, transformation de Fourier

Pour des fonction (pas forcément périodiques), à support infini, la transformation de Fourier est une généralisation de l’analyse en série de Fourier des fonctions périodiques.
On peut obtenir le spectre fréquentiel S(f) d’un signal temporel s(t) en calculant la transformée de Fourier de la fonction s(t) :

\displaystyle S(f) = \int _{-\infty }^{+\infty }s(t)\,\mathrm {e} ^{-{\rm {i}}2\pi f t}\,\mathrm {d} t
Et on peut retrouver le signal temporel à partir du spectre en réalisant la Transformée de Fourier inverse

\displaystyle s(t) = \int _{-\infty }^{+\infty }S(f)\,\mathrm {e} ^{+{\rm {i}}2\pi f t}\,\mathrm {d} f

Noter le changement du signe de l’argument de l’exponentielle
Remarque : il existe des variantes dans la définition de la transformée de Fourier, différentes notamment par la valeur du coefficient de normalisation en facteur de l’intégrale, et/ou par le choix de la variable choisie pour représenter le spectre (la fréquence (f ou \nu), ou bien la pulsation \omega).
En savoir (beaucoup) plus sur wikipedia . Remarque : Dans la page Wikipedia, la fréquence est, comme souvent en physique, notée \nu (“nu”) au lieu de f.
Pour les étudiants du BUT GIM, le cours sur la Transformée de Fourier sera vu en math en BUT 3.

10.5 Analyse FFT des signaux numériques de durée finie

Avertissement: Dans ce qui suit, on ne développe pas les aspects historiques, mathématiques, ni algorithmiques. On se limite aux aspects pratiques de l’analyse fréquentielle des supports numériques, du point de vue d’un utilisateur de logiciels d’analyse ou d’appareils de mesure.

Temps discret : L’échantillonnage revient à définir le temps de manière discrète au lieu du temps continu. Cela conduit à adapter les principes développés précédemment, et définir la Transformée de Fourier des signaux Discrets.
Frequence maximum : Une des conséquences de l’échantillonnage est que l’on ne peut analyser correctement que des signaux dont la fréquence maximum est inférieure à F_e/2.
Spectre discret : Une autre conséquence est notamment que le spectre est aussi défini de manière discrète, et que l’on ne peut pas connaître le spectre de façon continue.
Durée finie : En pratique, les signaux numériques sont en pratique à support temporel fini, alors que la transformée de Fourier a été définie pour des signaux à support infini, cela a aussi des conséquences sur l’analyse des signaux.
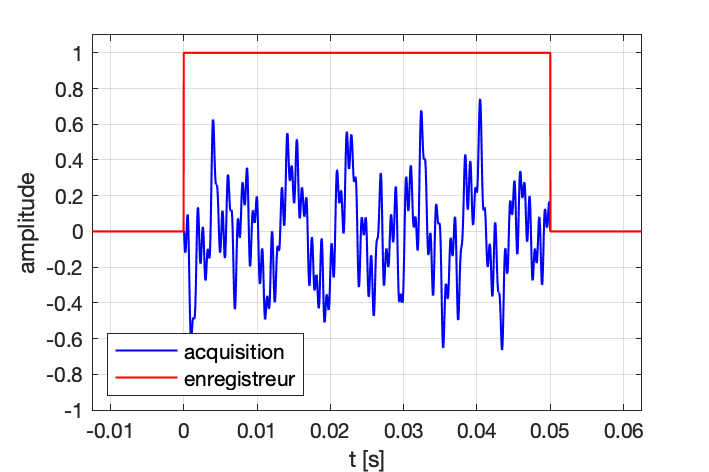
FFT : Plusieurs algorithmes permettent de calculer la transformé de Fourier discrète. Le plus couramment utilisé par les logiciels d’analyse et les apppareil de mesure est l’algorithme Fast Fourier Transform, communément appelé FFT.
On se place dans la suite dans la situation où un signal a été enregistré pendant une durée finie T, et numérisé à une fréquence d’échantillonnage Fe. On ne prête pas attention aux conséquences de la quantification (amplitude), ceci afin de se concentrer sur les aspects temporels et fréquentiels.

10.5.1 Théorème de Shannon, repliement (important !)

Le théorème de Shannon, appelé aussi Nyquist-Shannon, ou encore théorème de l’échantillonnage, énonce que l’échantillonnage d’un signal exige un nombre d’échantillons par unité de temps supérieur au double de l’écart entre les fréquences minimale et maximale qu’il contient.
En pratique, comme il est fréquent que la fréquence minimale est très inférieure à la fréquence maximale, voire qu’elle est nulle (si composante continue), on retiendra qu’il faut que la fréquence d’échantillonnage soit supérieure au double de la plus haute fréquence du signal F_{max} :

\boxed{F_e > 2 \ F_{max}}
- On peut aussi dire de manière équivalente :
\boxed{F_{max} < F_e / 2 \ }
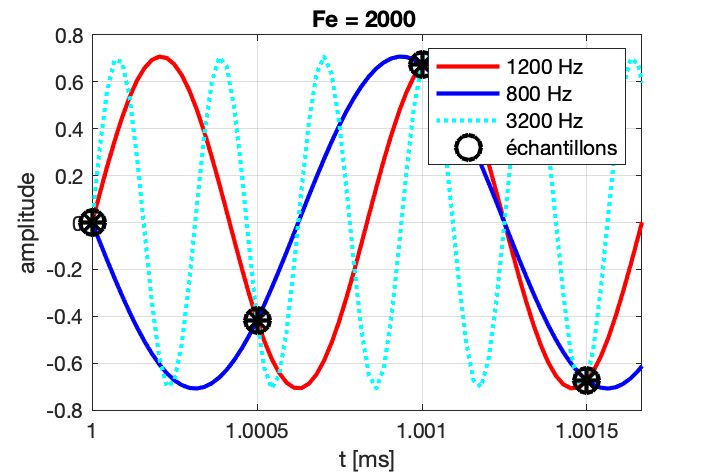
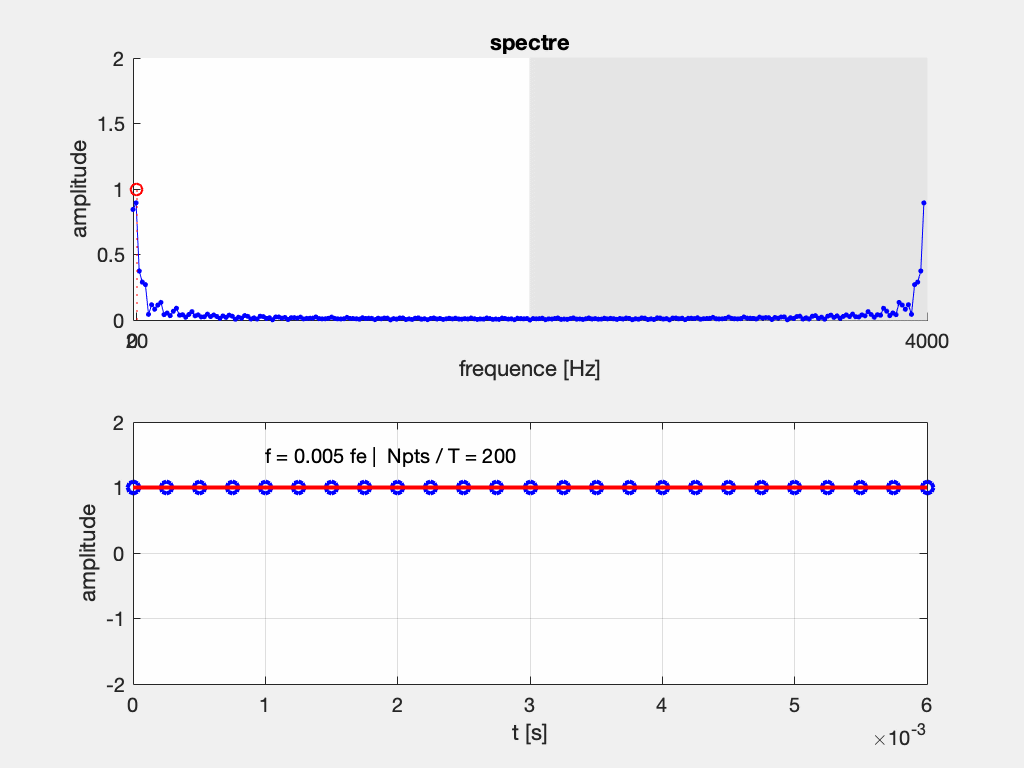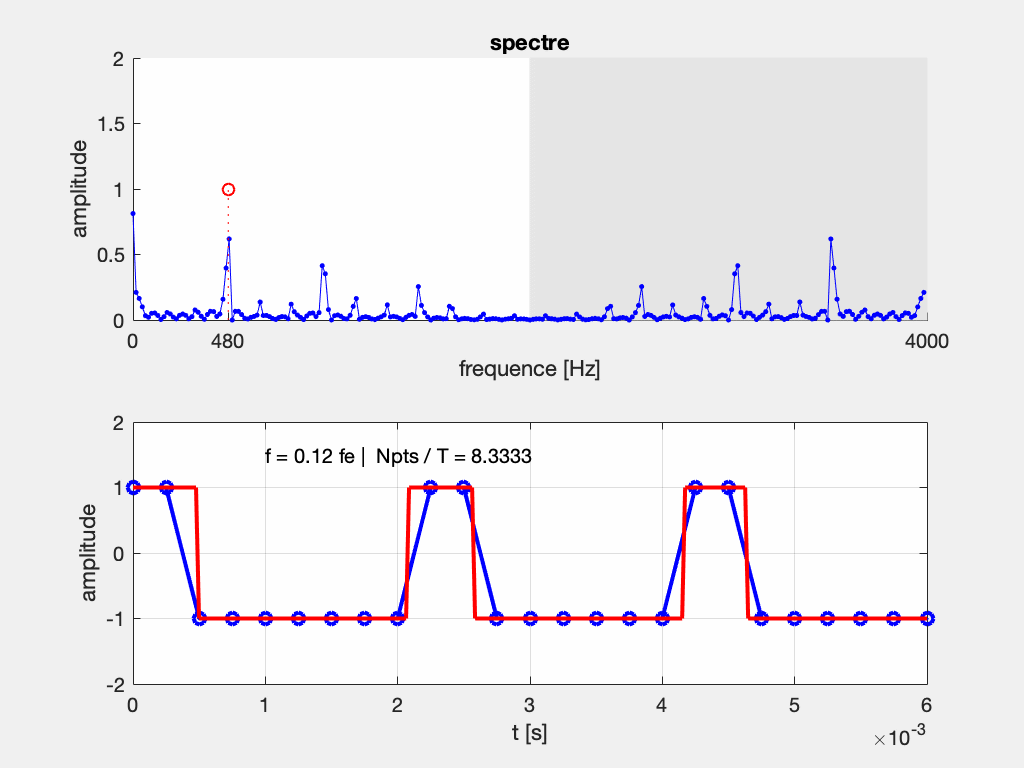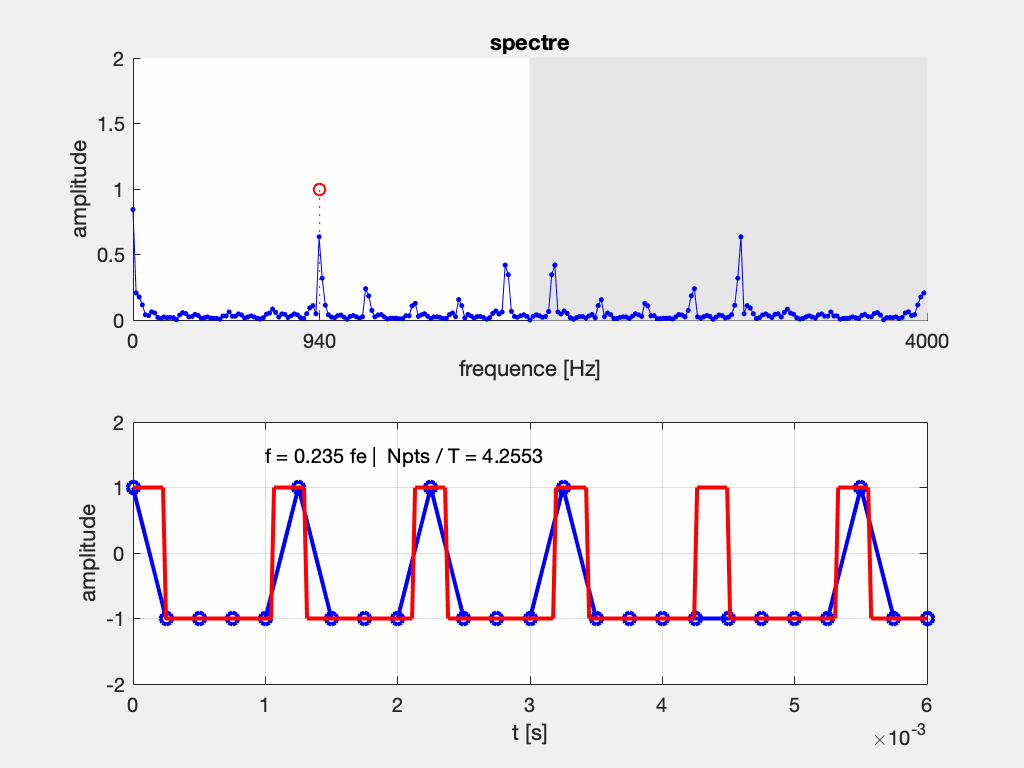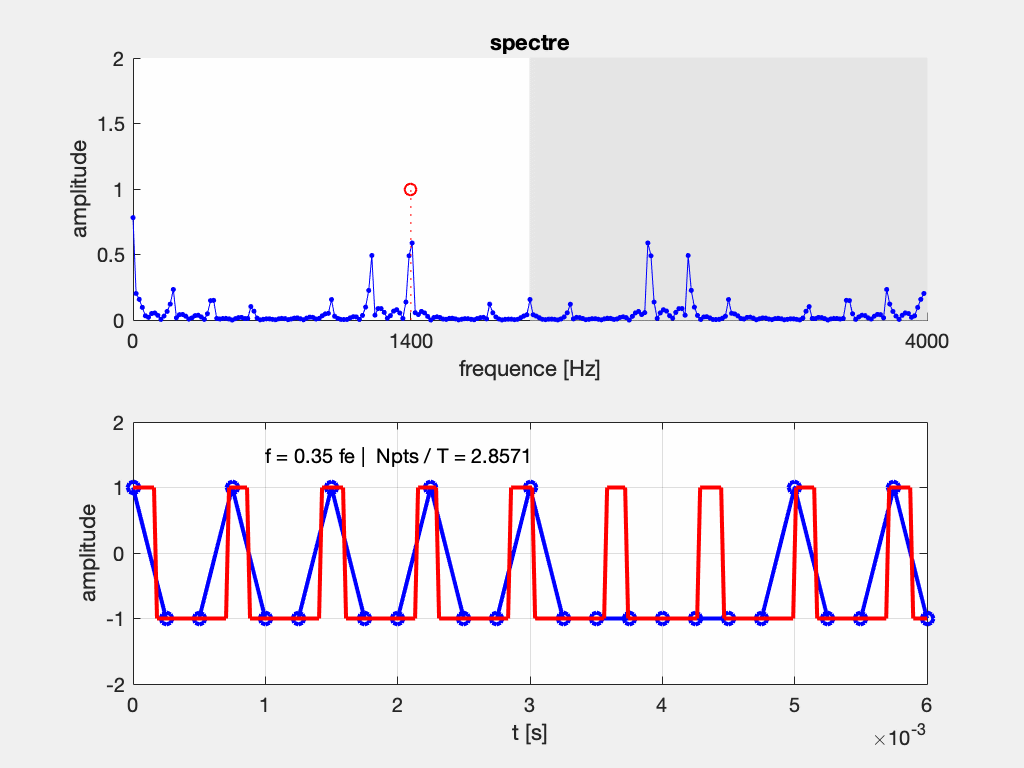
Que se passe-t-il si le théorème de Shannon n’est pas respecté, et que l’on relève moins de 2 échantillons par période ?
- Si on considère l’exemple d’un échantillonnage à Fe = 2000 Hz d’un signal à F = 800 Hz, on s’apperçoit que plusieurs sinusoïdes passent par ces points. Elles sont telles que leur fréquence vaut (\pm n F_e) \pm F, c’est-à-dire : (\pm) 800 Hz, 1200 Hz, 2800 Hz, 3200 Hz, 4800 Hz, …
- C’est comme si le spectre était “périodisé”, tous les F_e, à quoi s’ajoute la symmétrie autour de 0, \pm F_e, \pm 2 F_e, etc.
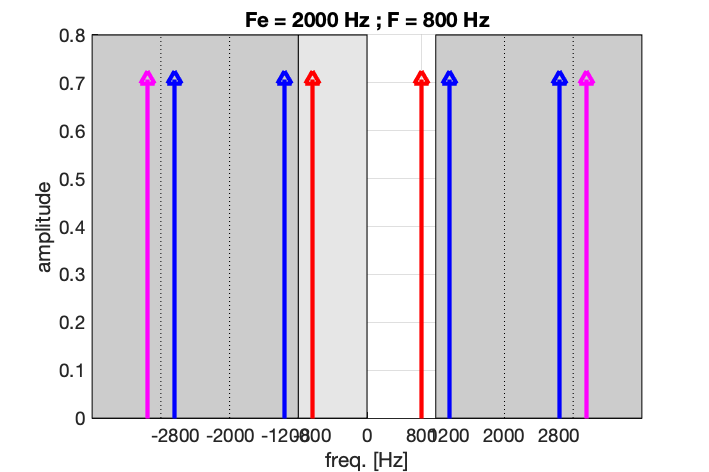
- En pratique, on n’affiche sur les appareils de mesure que les composantes entre 0 et F_e/2, soit ici entre 0 et 1000 Hz.
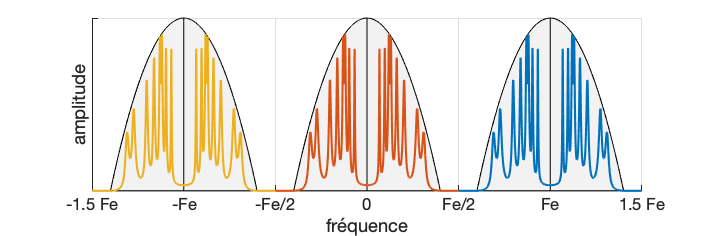
- Si maintenant on ne respecte pas le théorème de Shannon, avec un échantillonnage à Fe = 2000 Hz d’un signal à F = 1200 Hz, on s’apperçoit que plusieurs sinusoïdes passent par ces points. Elles sont telles que leur fréquence vaut (\pm n F_e) \pm F, c’est-à-dire : (\pm) 800 Hz, 1200 Hz, 2800 Hz, 3200 Hz, 4800 Hz, …
- Et comme le signal que l’on peut reconstruire à partir des points échantillonnés sera cette fois la sinusoïde à 800 Hz, … on ne va pas analyser la bonne fréquence !
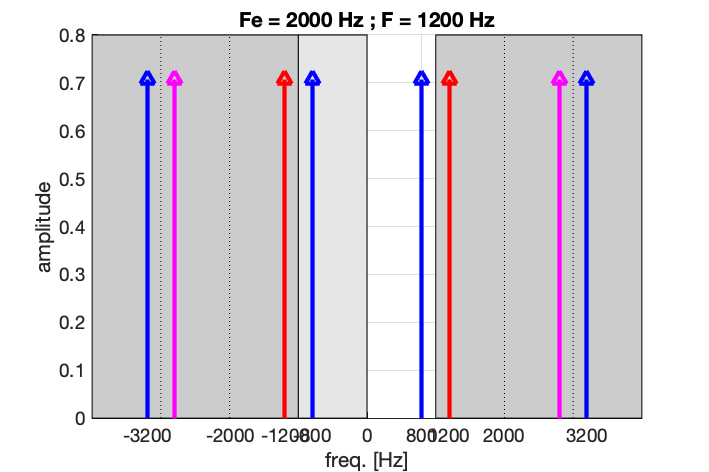
- On parle alors alors de repliement du spectre. En anglais, cet “effet mirroir” est appelé aliasing.
```
  ajouter figure
```
- On peut interpréter le repliement du spectre comme une conséquence de sa périodisation.
```
  ajouter figure
```
Pour éviter ce phénomène, la plupart des cartes d’acquisition de qualité ont un filtre passse-bas spécifiquement conçu pour filtrer les fréquences supérieures à F_e/2 et éviter le repliement du spectre. On appelle ces filtres des Filtres anti-repliement (ou anti-aliasing)
```
  ajouter figure
```
Mais tous les appareils n’en sont pas équipés. En particulier, beaucoup d’oscilloscope numériques proposent une fonction d’analyse du spectre (FFT), mais n’ont pas de filtre anti-repliement. Voilà ce qui peut se passer si vous analysez des fonctions à fréquence variable (balayage fréquentiel, ou frequency sweep) sur un oscilloscope numérique sans filtre anti-repliement :

10.5.2 Résolution fréquentielle

10.5.3 Troncature - Fenêtres de pondération

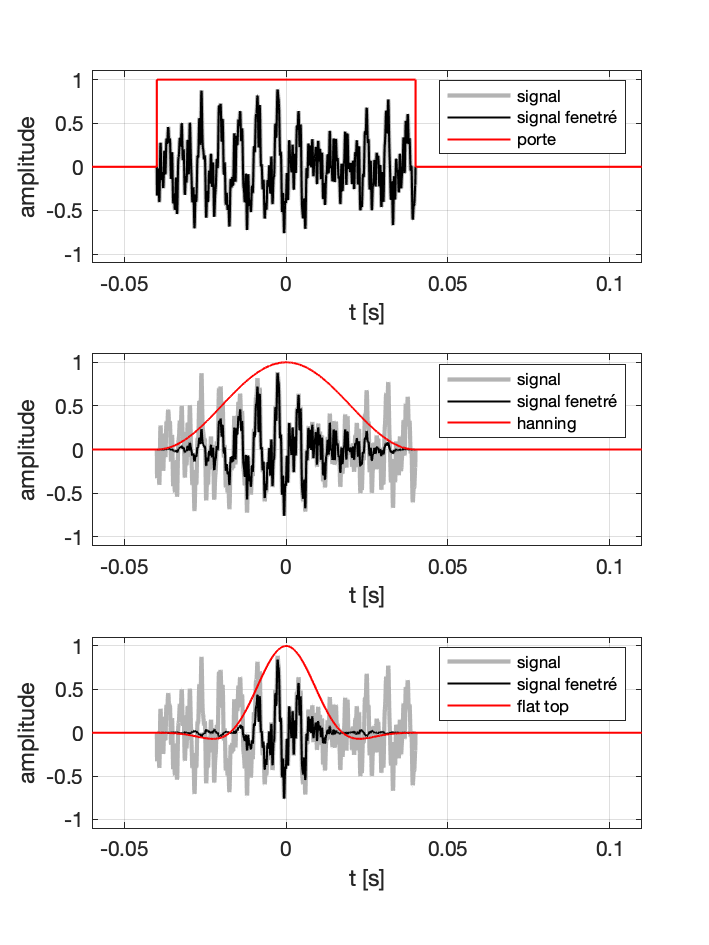
Pour limiter les artefacts dus à la troncature du signal (qui est en pratique tronqué, c’est-à-ire de dirée finie), on “adoucit” les disccontinuités au début et à la fin de l’enregistrement.
Pour cela on applique ce que l’on apppelle des fenêtres de pondération qui donnenent moins de “poids” au début et à la fin de l’enregistrement.
Les fenêtre les plus courantes sont : la fenêtre dite carrée, la fenêtre de Hann (ou Hanning), la fenêtre dite flat top (dessus plat).
On utilise aussi d’autres fenêtres dans certains cas : Hamming, Tuckey, Blackman, …
Les fenêtre de pondération ont pour effet notamment de midifier la forme des pics du spectre
En général, si on ne connaît ni précisément la fréquence, ni l’amplitude des phénomènes observés, on choisit généralement une fenêtre de pondération de type Hann (appelée aussi Hanning).
Si on connaît précisément la fréquence (par exemple parce que l’on connaît la fréquence d’excitation d’un système), alors on peut préférer une fenêtre de pondération de type “Flat Top”.