1 Introduction

Dans ce chapitre, on s’intéresse au mouvement de systèmes solides indéformables ou d’ensembles de solides indéformables.

Pour cela, on décomposera les mouvements des solides en mouvements de translation et mouvement de rotation.

---

2 Rappels

2.1 Coordonnées

• Pour repérer les mouvements dans l’espace, il faudra connaitre 6 coordonnées :

  • 3 coordonnées pour la translation
  • 3 coordonnées pour la rotation

• Pour décrire un mouvement plan, il faudra connaître 3 coordonnées

  • 2 coordonnées pour la translation dans le plan
  • 1 coordonnées pour la rotation d’axe perpendiculaire au plan

Figure: 6 degrés de liberté ou de liaison : 3 translations et 3 rotations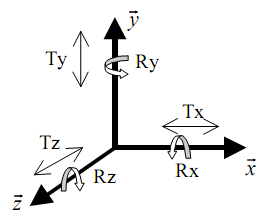

2.2 Référentiel

• On choisit un référentiel principal de l’étude, si possible Galliléen fixe ou considéré comme tel pendant l’observation ou en translation uniforme)

• Il arrivera le plus souvent que l’on définisse des référentiels ou repères iés aux différents solides qui constituent un ensemble mécanique en mouvement.

• On précisera donc dès que nécessaire par rapport à quel référentiel \mathcal{R} sont exprimés les vitesses et laccélérations :

• Par exemple pour la vitesse d’un point A par rapport à un référentiel \mathcal{R} on notera : \overrightarrow{\Gamma}_{A\in S/\mathcal{R}}

---

2.3 Solide indéformable

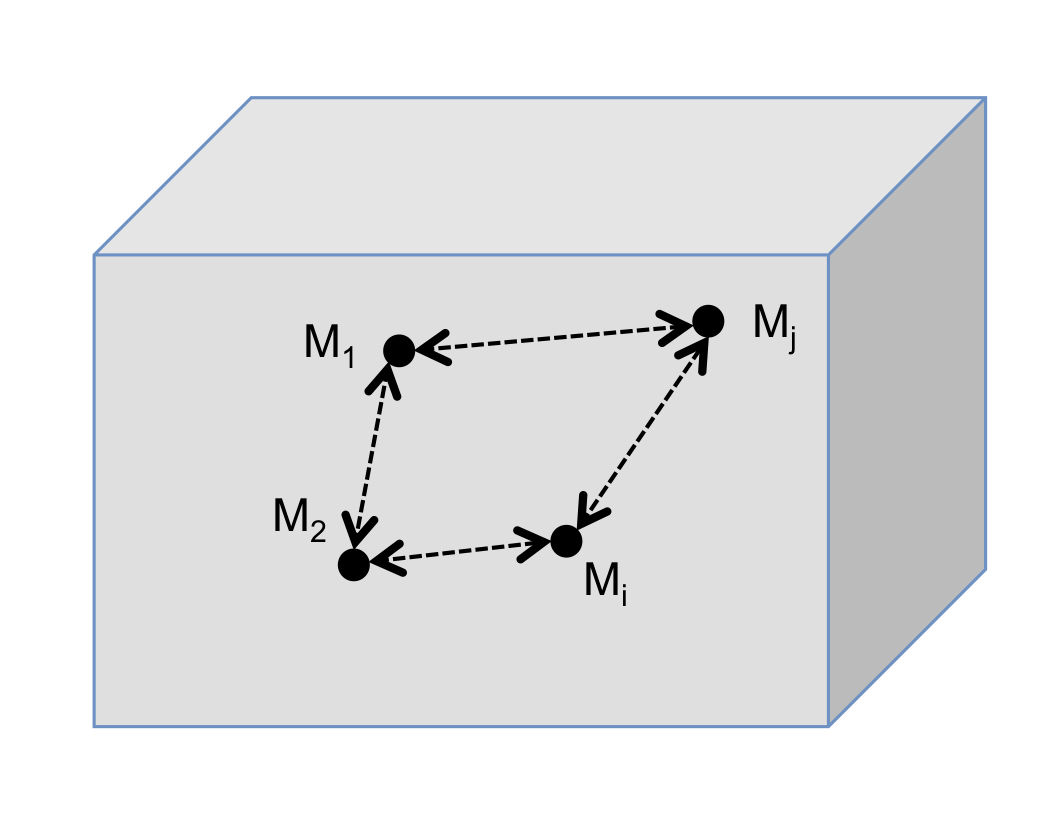
Soit (S) un ensemble fini ou infini de points: M_1, M_2, …, M_i,…, M_j, …, etc. Si, quels que soient i et j, les distances M_iM_j sont constantes à tout instant, alors (S) constitue un solide indéformable.

---

3 Mouvements d’un solide

3.1 Translation

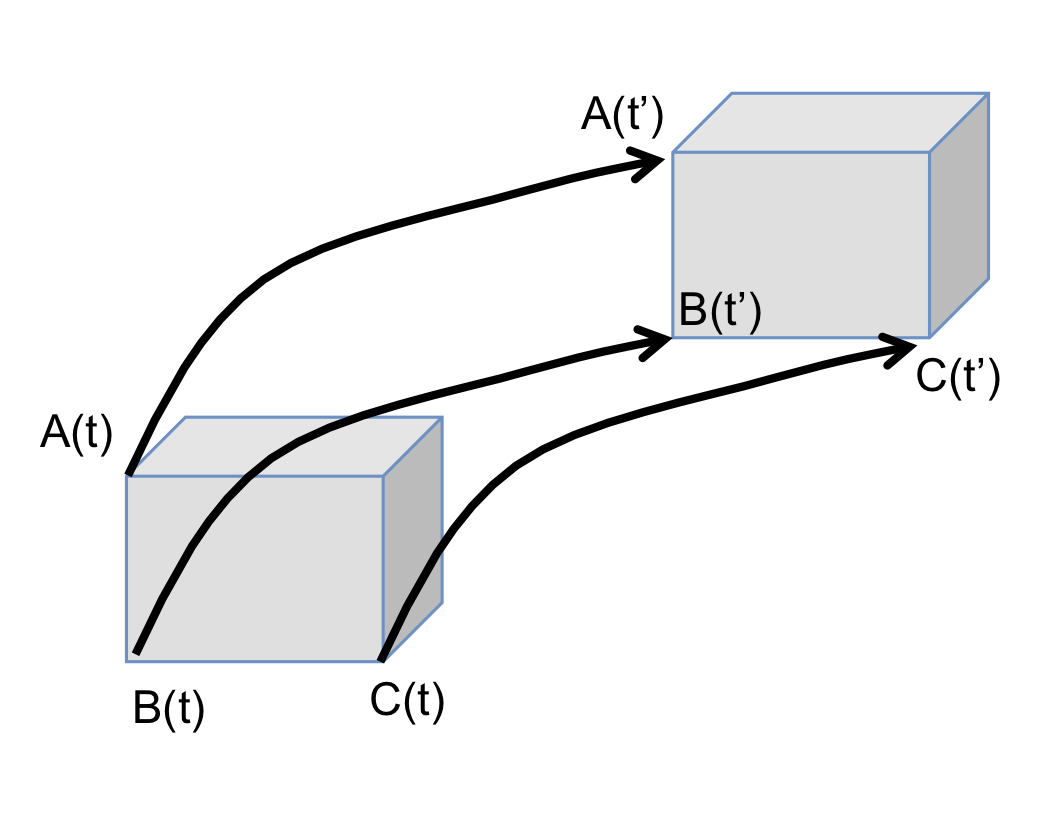
On considère des points A, B, C d’un solide indéformable.

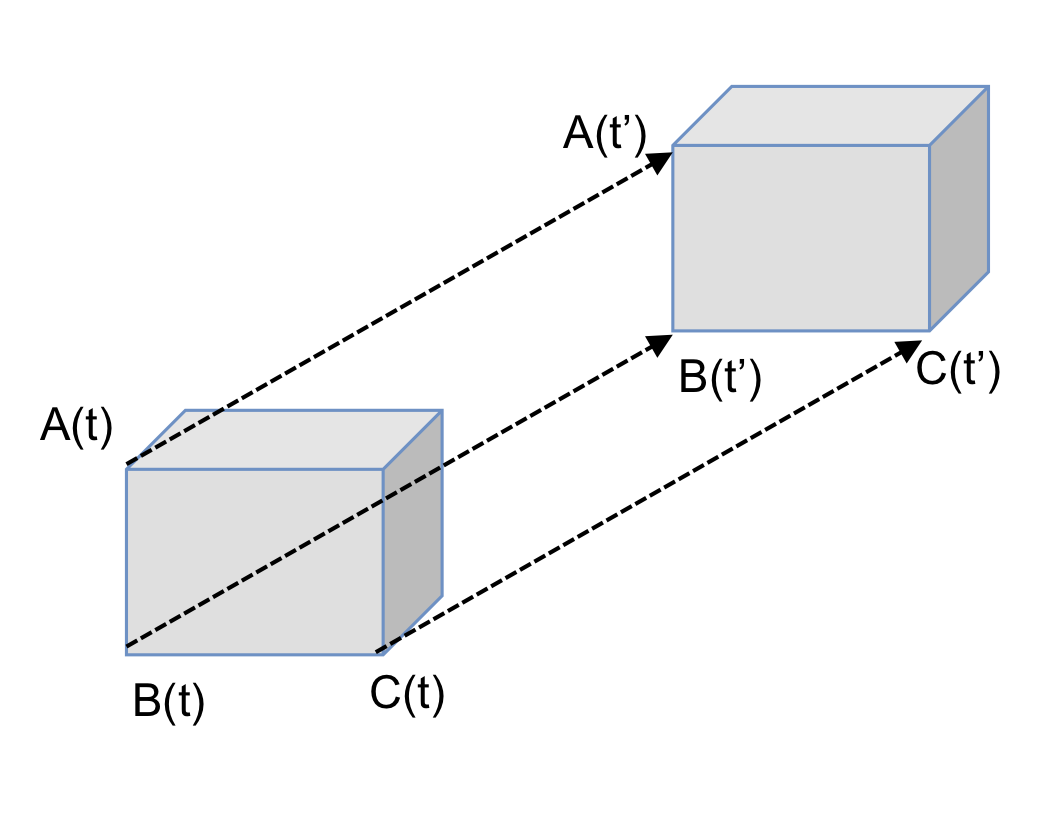
Il y a mouvement de translation si, quels que soient les instants t et t', tous les points se déplacent à la même vitesse \overrightarrow{v}_S et subissent la même accélération \overrightarrow{\Gamma}_S :

\overrightarrow{A(t)A(t')}=\overrightarrow{B(t)B(t')}=\overrightarrow{C(t)C(t')} \overrightarrow{v}_{A\in (s)/\mathcal{R}}=\overrightarrow{v}_{B\in (s)/\mathcal{R}}=\overrightarrow{v}_{C\in (s)/\mathcal{R}}=\overrightarrow{v}_{(s)/\mathcal{R}} \overrightarrow{\Gamma}_{A\in (s)/\mathcal{R}}=\overrightarrow{\Gamma}_{B\in (s)/\mathcal{R}}=\overrightarrow{\Gamma}_{C\in (s)/\mathcal{R}}=\overrightarrow{\Gamma}_{(s)/\mathcal{R}}

3.1.1 Cas particuliers

• Translation rectiligne : il y a translation rectiligne si la trajectoire des points de (S) est une droite, c’est-à-dire si \overrightarrow{\Gamma}_{A\in S/\mathcal{R}} \ // \ \overrightarrow{v}_{A \in S/\mathcal{R}} \ \ \forall \ \ A \ \in (S).

    insérer gif : chariot

  

  

• Translation curviligne : Tous les points ont des trajectoires courbe superposables.

• Translation uniforme : il y a translation uniforme si ||\overrightarrow{v}_S|| est constant, c’est-à-dire si \overrightarrow{\Gamma}_{A\in S/\mathcal{R}} = \vec{0} ou si \overrightarrow{\Gamma}_{A\in S/\mathcal{R}} \ \perp \ \overrightarrow{v}_{A\in S/\mathcal{R}}.

---

A retenir :

Si un solide (s) est uniquement en translation, alors :

• tous les points se déplacent à la même vitesse \overrightarrow{v}_S
• il ont la même accélération $_S
• leurs trajectoires sont superposables

---

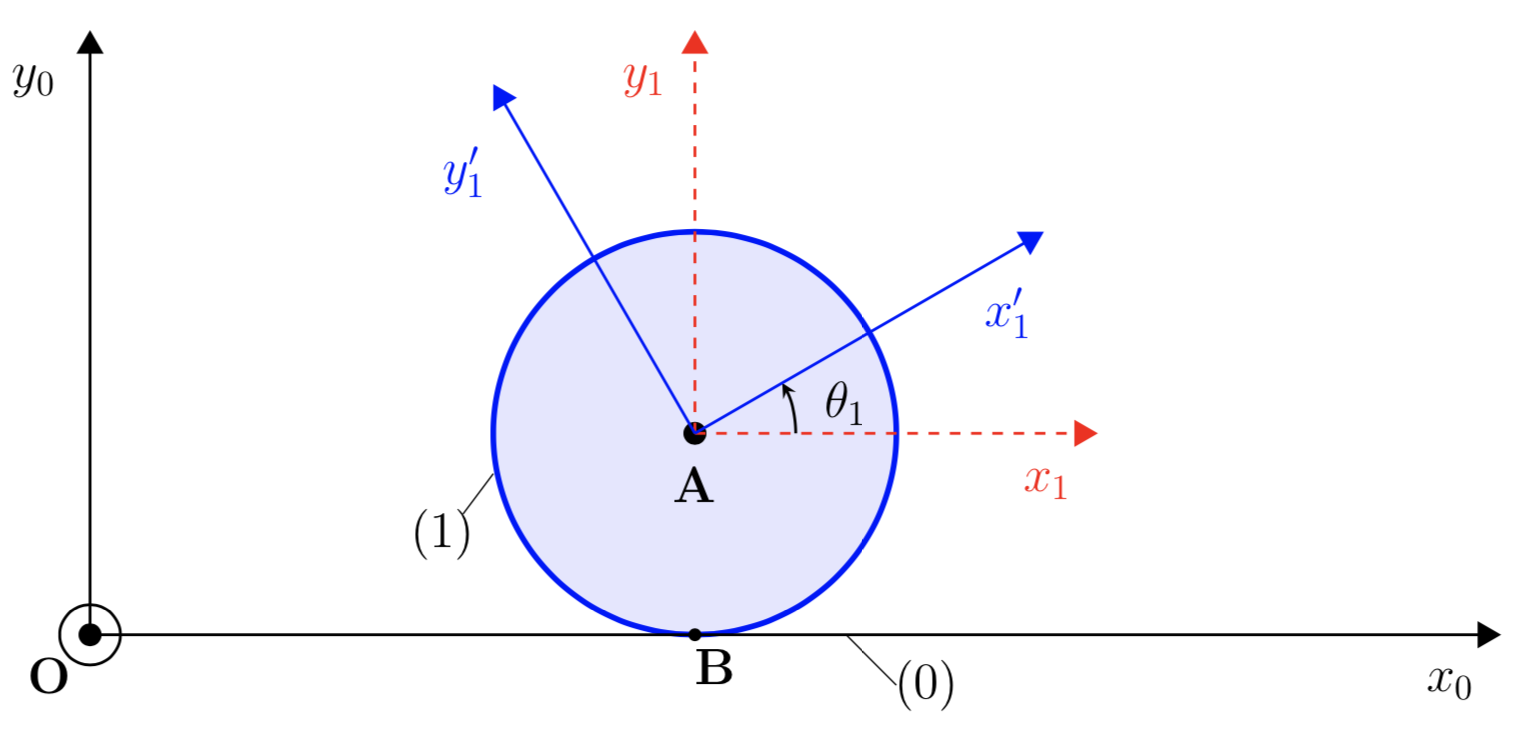
3.2 Rotation autour d’un axe fixe

---

---

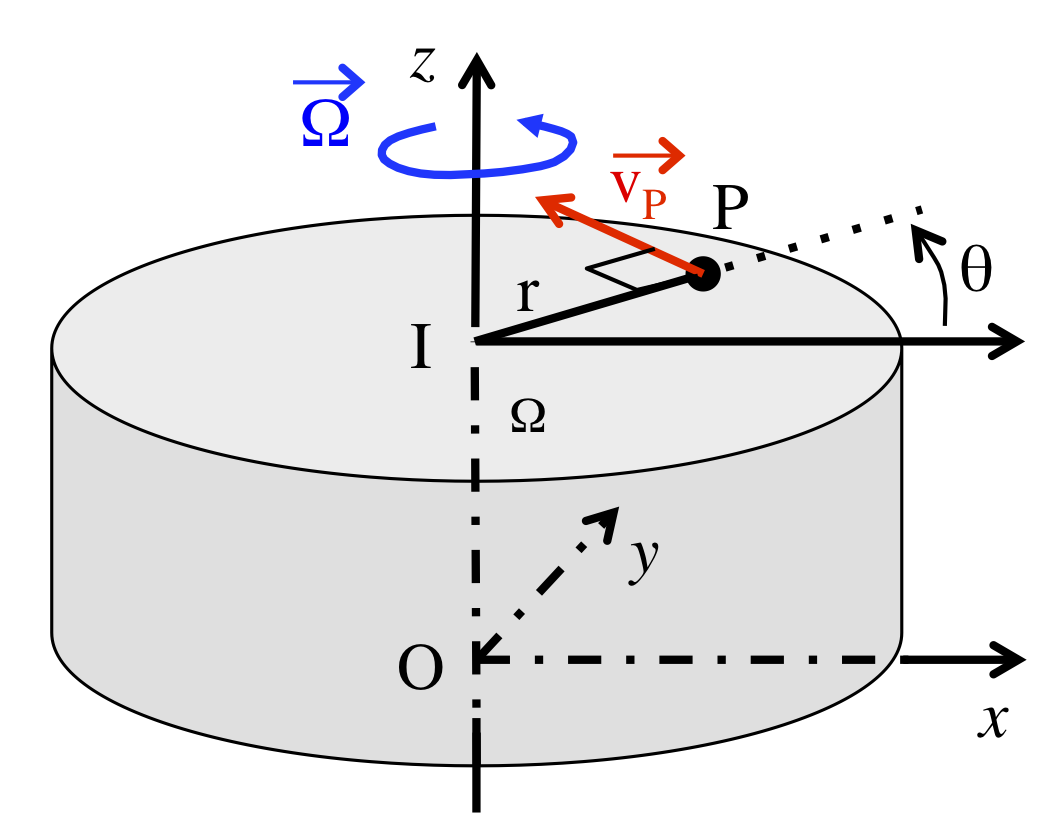
S’il y a rotation autour d’un axe fixe, tous les point du solide ont une trajectoire circulaire dans un plan perpendiculaire à l’axe de rotation

Si, comme indiqué sur la figure ci-desssus, on définit un référentiel \mathcal{R}=(Ox,Oy,Oz), les coordonnées cylindriques de base (\vec{u},\vec{v},\vec{k}) en positionnant l’axe Oz selon l’axe de rotation, et si on considère un point P \in(S), alors on peut écrire :

• Le vecteur rotation

\boxed{ \ \overrightarrow{\Omega}_{(s)/\mathcal{R}}= \begin{pmatrix} 0 \\ 0 \\ \dot{\theta} \end{pmatrix} \ }

• Le vecteur position: \overrightarrow{OP}=\overrightarrow{OI}+\overrightarrow{IP}=OI \ \vec{k}+IP \ \vec{u}.

• On déduit le vecteur vitesse :
  \vec{v}_{P/\mathcal{R}}=\frac{\rm{d} \ \overrightarrow{OP}}{\rm{d}t}=\frac{\rm{d} \ (OI \ \vec{k}+IP \ \vec{u})}{\rm{d}t} \ \ \Longrightarrow  \boxed{ \vec{v}_{P/\mathcal{R}}=IP \ \dot{\theta} \ \vec{v}} en remarquant : \frac{\rm{d}\ \vec{k}}{\rm{d}t}=\vec{0}   ; \ \ \frac{\rm{d} \ OI}{\rm{d}t} = 0 \ ; \ \ \frac{\rm{d} \ IP}{\rm{d}t} = 0 \ ; \ \ \frac{\rm{d} \ \vec{u}}{\rm{d}t}=\dot{\theta} \vec{v}

• Remarque importante:
  Si I \in Oz (axe de rotation), on peut obtenir ce résultat en calculant \overrightarrow{\Omega}_{(s)/\mathcal{R}}\wedge\overrightarrow{IP} ou \overrightarrow{PI}\wedge\overrightarrow{\Omega}_{(s)/\mathcal{R}} :
  \boxed{ \vec{v}_{P\in (s)/\mathcal{R}} = \overrightarrow{PI}\wedge\overrightarrow{\Omega}_{(s)/\mathcal{R}} = \overrightarrow{\Omega}_{(s)/\mathcal{R}}\wedge\overrightarrow{IP} = IP \ \dot{\theta} \ \vec{v} }

• N.B.: Dans la formule précédente, on peut remplacer le point I par n’importe quel point de l’axe, et dans le cas présent, par O. Si l’axe de rotation est Oz, le vecteur rotation est \overrightarrow{\Omega}=\dot{\theta} \ \vec{k}. Le vecteur position est \overrightarrow{OP}=OI \ \vec{k}+IP  \vec{u} (voir la figure ci-dessus). On écrit alors \begin{matrix} \overrightarrow{\Omega}\wedge\overrightarrow{OP} & = & \dot{\theta}\vec{k}\wedge(OI\vec{k}+IP\vec{u}) \\ & = & OI\dot{\theta}(\vec{k}\wedge\vec{k})+\dot{\theta}IP(\vec{k}\wedge\vec{u}) \\ & = & \overrightarrow{0}+\dot{\theta}IP(\vec{k}\wedge\vec{u}) \\ & = & IP \ \dot{\theta} \ \vec{v} \end{matrix}

---

Généralisation :

Si B est un point d’un solide en rotation avec une vitessse \overrightarrow{\Omega}_{(s)/\mathcal{R}} autour d’un axe fixe par rapport à un référentiel \mathcal{R}, et A est un point situé sur l’axe, alors la vitesse \overrightarrow{v}_{B\in (s)/\mathcal{R}} du point B est liée à la vitesse de A \overrightarrow{v}_{A\in (s)/\mathcal{R}} et à la vitessse de rotation \overrightarrow{\Omega}_{(s)/\mathcal{R}} : \boxed{ \vec{v}_{B\in (s)/\mathcal{R}} = \overrightarrow{BA}\wedge\overrightarrow{\Omega}_{(s)/\mathcal{R}} }

// to do :  insérer une figure 
            insérer un exemple d'application : //

---

Exercices d’application :

1. Un rotor de diamètre 10 cm tourne à la frequence de 30 Hz.
   Question: Quelle est la vitesse de translation d’un point de la surface du rotor ?

2. Un cylindre de diamètre 10 cm tourne sur un tour d’usinage à la vitesse de 360 tours par minute.
   Question: Quelle est la vitesse de coupe ? (vitesse relative d’un point de la surface / à l’outil supposé fixe)

3. Un vélo dont les roues ont un diamètre de 28 pouces avance à la vitesse de 20 km/h.
   Questions:

   • Quelle est la vitesse de rotation des roues ?
   • Quelle est la vitesse de rotation d’un second vélo, avançant à la même vitesse, mais avec des roures de 26 pouces ?

---

A retenir :

• S’il y a rotation autour d’un axe fixe, tous les points du solide ont une trajectoire circulaire dans un plan perpendiculaire à l’axe de rotation

• La vitesse de translation d’un point en rotation par rapport à un axe a pour module le rayon \times module de la vitesse de rotation

• Le vecteur rotation a pour direction l’axe de rotation, et pour module la dérivée par rapport au temps de la position angulaire. L’unité du module la vitesse de rotation est le radian par seconde.

• Si rotation autour d’un axe fixe  \mathcal{R}, et A \in axe, alors : \boxed{ \vec{v}_{B\in (s)/\mathcal{R}} = \overrightarrow{BA}\wedge\overrightarrow{\Omega}_{(s)/\mathcal{R}} }

---

3.3 Cas général de mouvement d’un solide : Translation + Rotation

Dans le cas général, on peut décomposer le mouvement en une TRANSLATION combinée à une ROTATION :

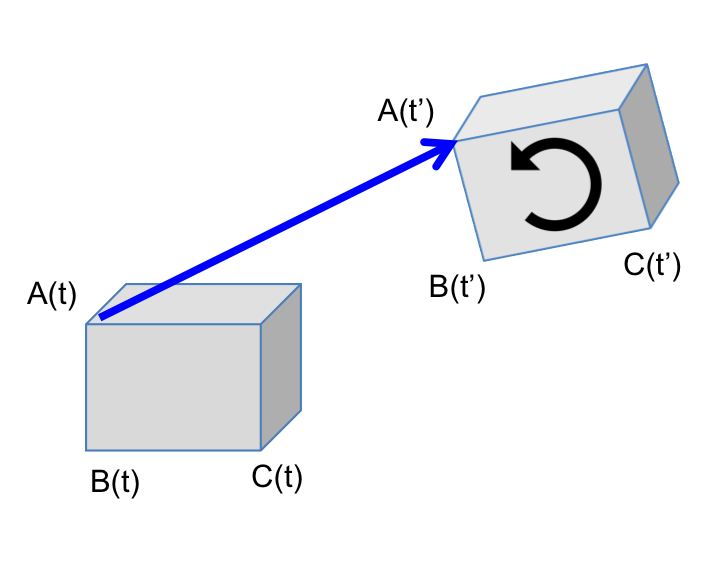
En se basant sur les relations précédentes, on déduit la relation entre les vitesse des points du solide sous la forme de la formule de Varignon déjà vue pour le transport des moments :

si A et B appartiennent au même solide, alors :

\boxed { \vec{v}_{B\in (s)/\mathcal{R}} = \vec{v}_{A\in (s)/\mathcal{R}} + \overrightarrow{BA}\wedge\overrightarrow{\Omega}_{(s)/\mathcal{R}} }

NB: Cette est formule très importante \Longrightarrow à connaitre par coeur

Moyen mnémotechnique : BABAR (vit. de B = vit. de A + BA prod. vect. Rotation)

On peut s’en rappeler en allégeant la notation : \vec{v}_B = \vec{v}_A + \overrightarrow{BA}\wedge\overrightarrow{\Omega} mais il ne faut pas oublier que A et B appartiennent au même solide, et que toutes les vitesses sont exprimées par rapport au même référentiel.

Cette formule permet de déterminer le champ des vitesses d’un solide à partir de la vitesse de translation d’un point, et de la vitesse de rotation

---

3.4 Torseur cinématique - définition

Le torseur cinématique réduit en A décrit le champ des vitesses d’un solide (s) par rapport à un référentiel \mathcal{R} en rassemblant la vitesse de rotation \overrightarrow{\Omega}_{(s)/\mathcal{R}} et le vecteur vitesse \vec{v}_{A\in(s)/\mathcal{R}} :

\boxed{ \left\{ \mathcal{V}_{(s)/\mathcal{R}} \right\}_A = \begin{Bmatrix} \overrightarrow{\Omega}_{(s)/\mathcal{R}} \\ \vec{v}_{A\in(s)/\mathcal{R}} \end{Bmatrix} = \begin{Bmatrix} \Omega_x & v_{Ax} \\ \Omega_y & v_{Ay} \\ \Omega_z & v_{Az} \end{Bmatrix}_{\mathcal{R}} }

to do : insérer les exemples et figures

---

3.5 Transport d’un torseur (changement du point de réduction)

D’après les relations établies précédemment, à partir du torseur cinématique réduit en un point A, on peut déduire le torseur réduit en un point B :

\left\{ \mathcal{V}_{ (s)/\mathcal{R}} \right\}_B = \begin{Bmatrix} \overrightarrow{\Omega}_{(s)/\mathcal{R}} \\ \vec{v}_{B\in(s)/\mathcal{R}} \end{Bmatrix} = \begin{Bmatrix} \overrightarrow{\Omega}_{(s)/\mathcal{R}} \\ \vec{v}_{A\in(s)/\mathcal{R}}+\overrightarrow{BA}\wedge\overrightarrow{\Omega}_{(s)/\mathcal{R}} \end{Bmatrix}

3.6 Torseurs cinématique particuliers: Rotation pure / Translation pure / Mouvement plan

• Si le solide est uniquement en rotation par rapport à \mathcal{R}, alors :

\left\{ \mathcal{V}_{ (s)/\mathcal{R}} \right\}_A= \begin{Bmatrix} \overrightarrow{\Omega}_{(s)/\mathcal{R}} \\ \vec{0} \end{Bmatrix} = \begin{Bmatrix} \Omega_x & 0 \\ \Omega_y & 0 \\ \Omega_z & 0 \end{Bmatrix}

• Si le solide est uniquement en translation par rapport à \mathcal{R}, alors :

\left\{ \mathcal{V}_{ (s)/\mathcal{R}} \right\}_A= \begin{Bmatrix} \vec{0} \\ \vec{v}_{A\in(s)/\mathcal{R}} \end{Bmatrix} = \left\{ \begin{matrix} 0 & v_{Ax} \\ 0 & v_{Ay} \\ 0 & v_{Az} \end{matrix} \right\}

• (2D) : Si mouvement est contenu dans un plan, alors le vecteur rotation est perpendiculaire au plan contenant la trajectoire et les vecteurs vitesse

  Par exemple, si le mouvement est dans le plan (Ox,Oy) :

  \left\{ \mathcal{V}_{ (s)/\mathcal{R}} \right\}_A= \begin{Bmatrix} \overrightarrow{\Omega}_{(s)/\mathcal{R}} \\ \vec{v}_{A\in(s)/\mathcal{R}} \end{Bmatrix} = \left\{ \begin{matrix} 0 & v_{Ax} \\ 0 & v_{Ay} \\ \Omega_z & 0 \end{matrix} \right\}

---

3.7 Mobilité et liaisons : lien avec le torseur cinématique et le Torseur des actions mécaniques

to do : Discussion sur la complémentarité Torseur cinématique / Torseur des actions mécaniques  

• liaisons sur wikipedia
  
• Torseur des actions mécaniques sur wikipedia
  
• Torseur cinématique sur wikipedia

---

3.8 Propriété d’équiprojectivité du champ des vitesses

L’équiprojectivité du champ des vitesses d’un solide peut s’énoncer comme :

La projection de \vec{v}_A sur AB est égale à la projection de \vec{v}_B sur AB

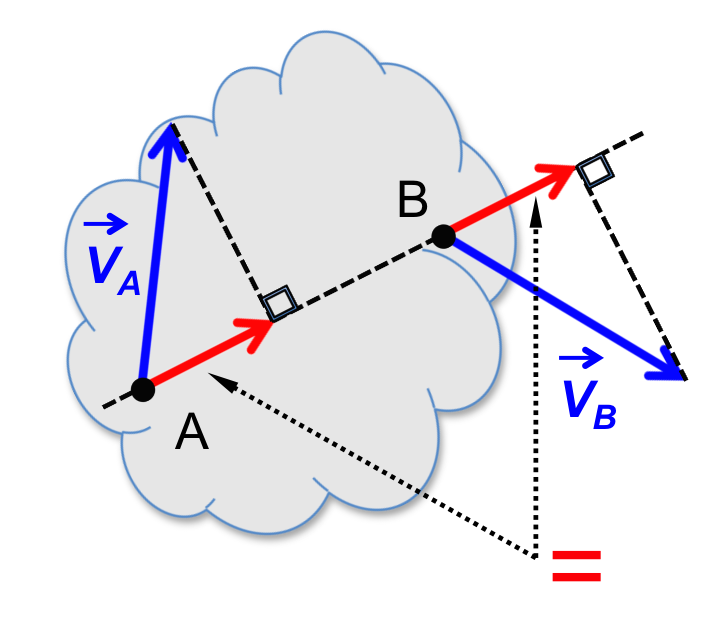
Important : A et B \in au même solide, et vitesses exprimées / au même référentiel \mathcal{R}

Remarque : Cette propriété peut être déduite en projetant la relation \vec{v}_{B\in (s)/\mathcal{R}} = \vec{v}_{A\in (s)/\mathcal{R}} + \overrightarrow{BA}\wedge\overrightarrow{\Omega}_{(s)/\mathcal{R}} sur AB, et on en déduit la relation sous cette forme : \boxed{ \overrightarrow{v}_{A\in (s)/\mathcal{R}}.\overrightarrow{AB} = \overrightarrow{v}_{B\in (s)/\mathcal{R}}.\overrightarrow{AB} }

3.8.1 Application

to do : 

1 - glissement d'une échelle
2 - syst bielle manivelle

---

3.9 Glissement - Roulement - Pivotement

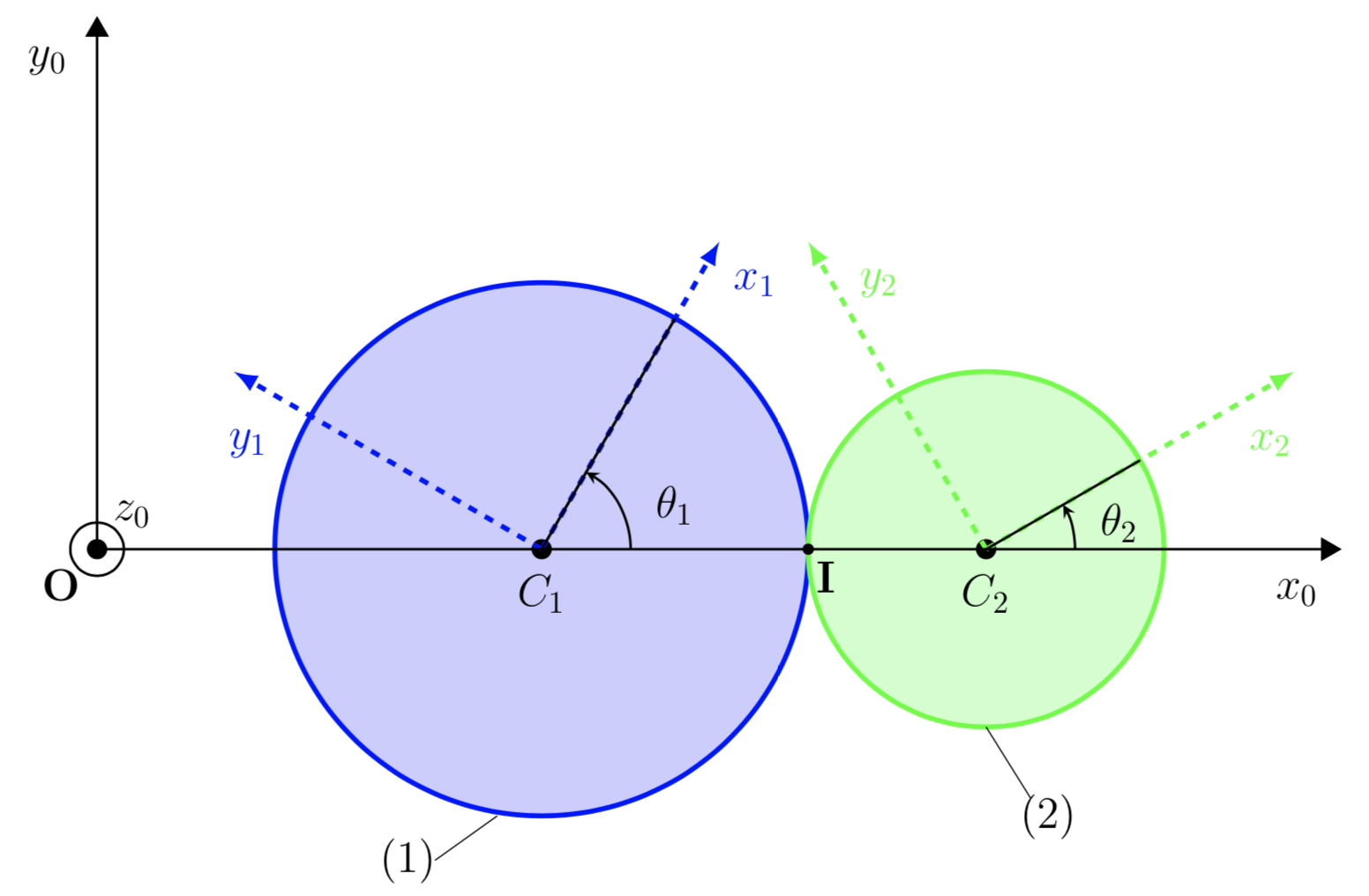
On considère deux solides (1) et (2) en contact en I.

On définit 3 vecteurs unitaires (\vec{t}_1,\vec{t}_2,\vec{n}) tels que:

(\vec{t}_1,\vec{t}_2) définissent le plan de contact entre (1) et (2), et \vec{n} \perp (\vec{t}_1,\vec{t}_2).

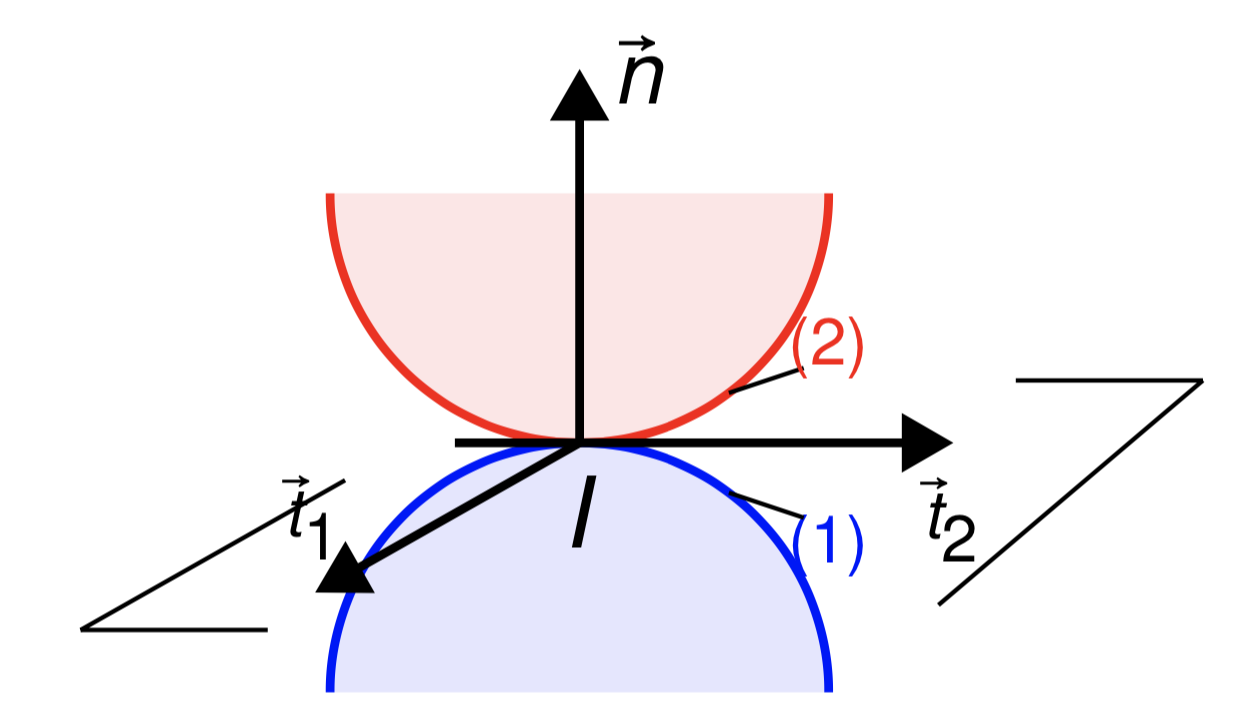
On identifie 3 types de mouvements qui peuvent être combinés : le Glissement, le Roulement, le Pivotement.

to do : insérer Animation 3D

---

3.9.1 Glissement

Le Glissement de (2) / (1) est le mouvement de Translation de (2) / (1) en I.

Ce mouvement est caractérisé par la vitesse de glissement qui est la vitesse relative \overrightarrow{v}_{I\in (2)/(1)} entre les deux solides au point(s) de contact :

\boxed{ \overrightarrow{v}_{I\in (2)/(1)} = \overrightarrow{v}_{I\in (2)/\mathcal{R}} - \overrightarrow{v}_{I\in (1)/\mathcal{R}} }

---

3.9.2 Roulement

Le Roulement de (2) / (1) un mouvement de Rotation} de (2) / (1)

Il est caractérisé par une vitesse de rotation \overrightarrow{\Omega}_{I\in (2)/(1)} telle que l’axe de rotation est contenu dans le plan de contact (\vec{t}_1,\vec{t}_2), il peut donc s’écrire : \boxed{\overrightarrow{\Omega}_{(2)/(1)}=\omega_1 \ \vec{t}_1 + \omega_2 \ \vec{t}_2}

---

3.9.3 Pivotement

Le Pivotement de (2) / (1) est le mouvement de rotation de (2) / (1)

Il est caractérisé par une vitesse de rotation \overrightarrow{\Omega}_{I\in (2)/(1)} telle que l’axe de rotation est perpendiculaire au plan de contact (\vec{t}_1,\vec{t}_2), il peut donc s’écrire : \boxed{\overrightarrow{\Omega}_{I\in (2)/(1)}=\omega \ \vec{n} }

---

3.9.4 Condition de non glissement

Il n’y a pas de glissement lorsque la vitesse relative au(x) point(s) de contact est nulle, c’est-à-dire si :

\boxed{\overrightarrow{v}_{I\in(2)/(1)}=\overrightarrow{v}_{I\in (2)/\mathcal{R}}-\overrightarrow{v}_{I\in (1)/\mathcal{R}} = \overrightarrow{0}}

ou autrement écrit : s \boxed{\overrightarrow{v}_{I\in (2)/\mathcal{R}}=\overrightarrow{v}_{I\in (1)/\mathcal{R}} }

IMPORTANT: La condition de roulement sans glissement permet de d’étudier la transmission des mouvements dans des mécanismes du type roulements, engrenages, entrainement par courroie ou chaine, crémaillère, came, etc.

to do : refaire les figures

---

3.10 Centre Instantané de Rotation (CIR)

Définition:

Pour tout solide en mouvement plan, il existe un et un seul point I tel qu’à un instant t sa vitesse est nulle: \overrightarrow{v}_I=\vec{0}

Ce point est appelé (CIR)

Remarques :

• Le CIR possède, à l’instant t, les propriétés d’un centre de rotation
  
• A l’instant suivant t+\Delta t, le CIR a changé de position géométrique
  
• Cette position varie au cours du temps et décrit une trajectoire
• Le CIR est un point géométrique qui n’est pas forcément un point du solide

Détermination du CIR :

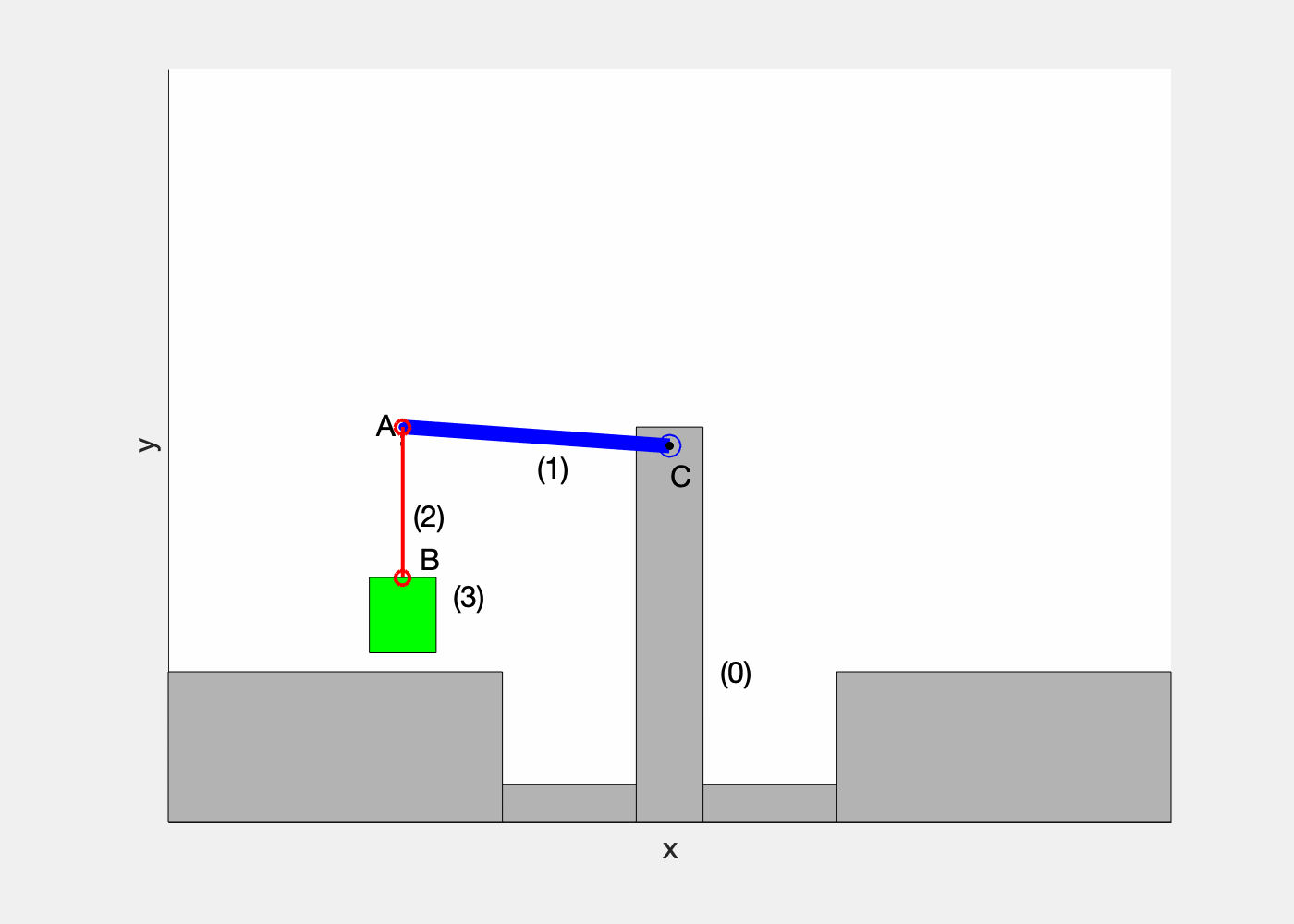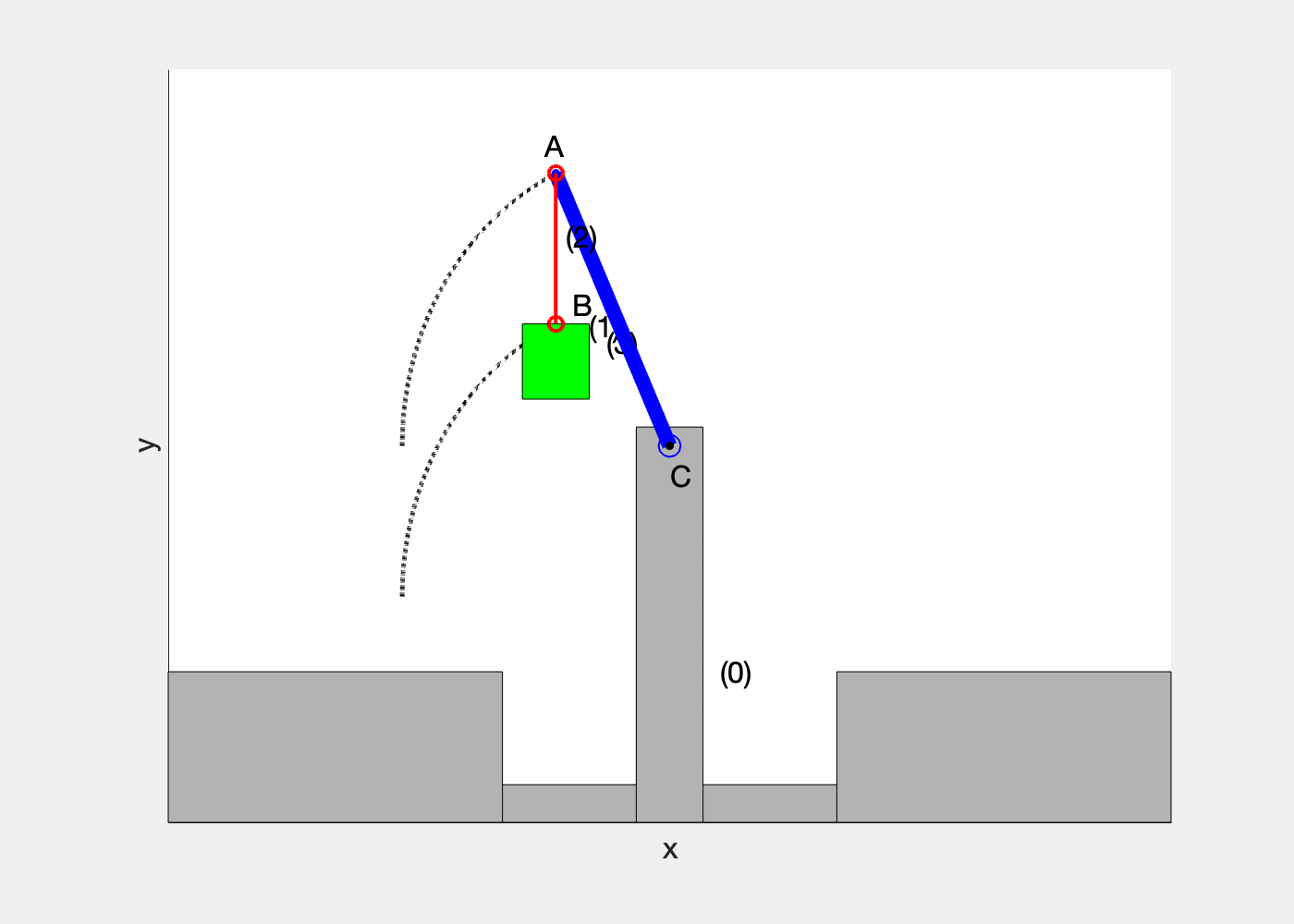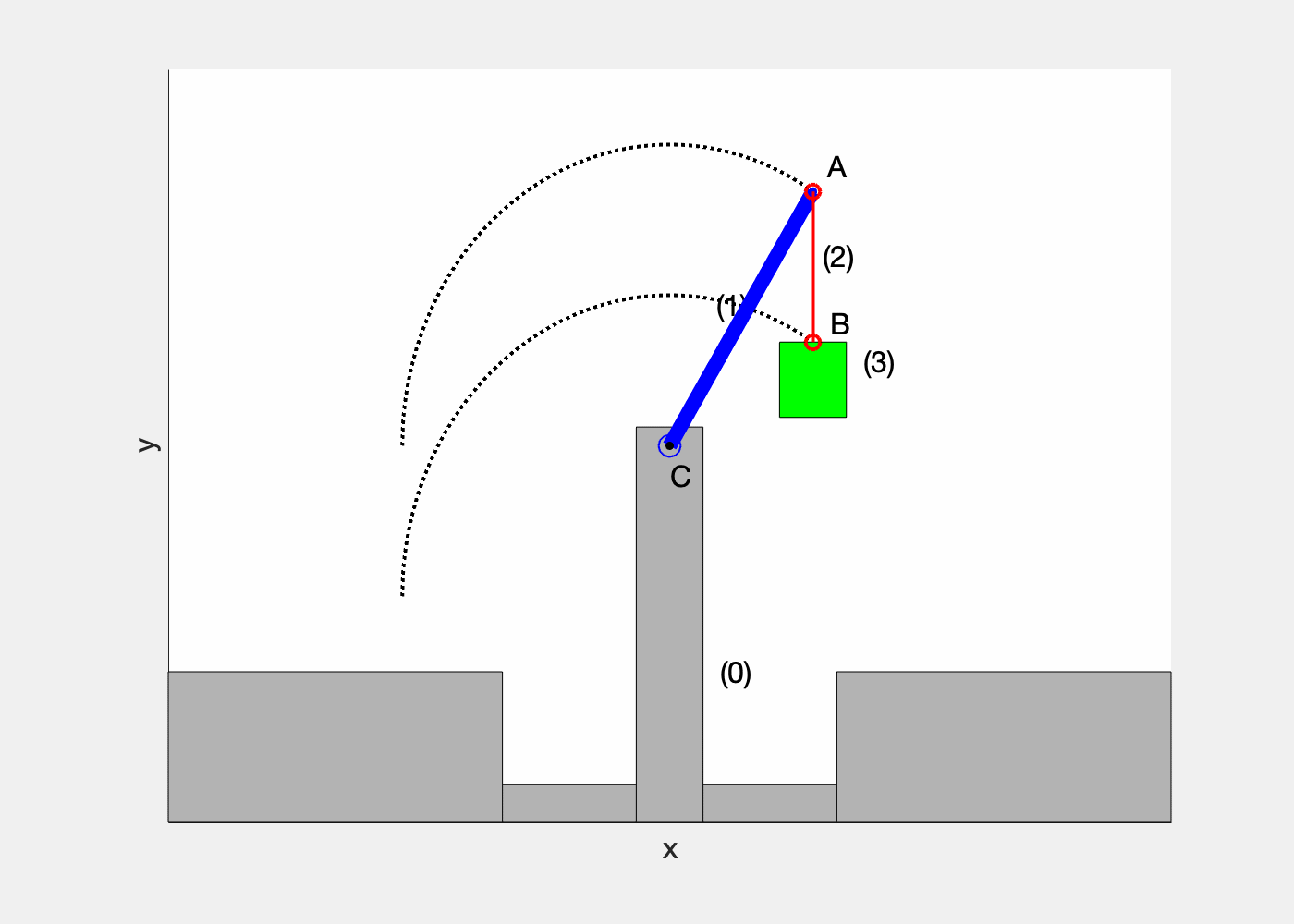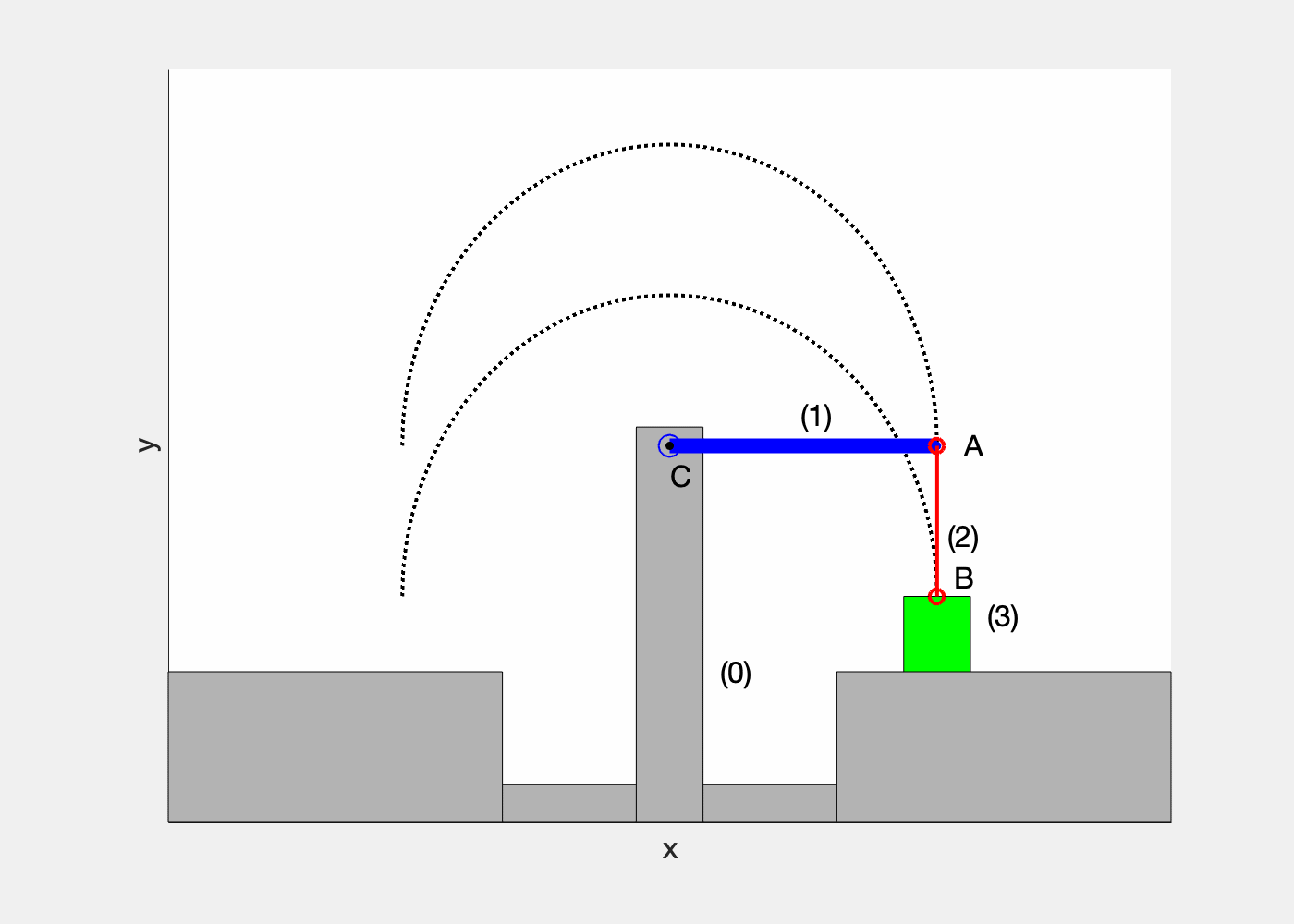
Le CIR I(t) est situé à l’intersection des perpendiculaires aux vecteurs vitesse passant par les points du solide (voir la figure ci-dessous)

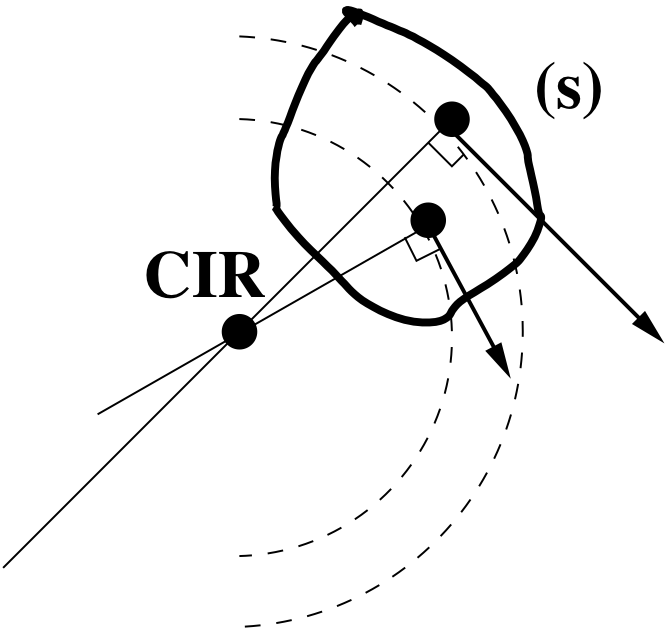
Relations importantes (à retenir) :

On considère trois points A, B, et C du solide (S)

Au temps t le solide est en rotation pure autour du CIR I à la vitesse de rotation instantannée \overrightarrow{\Omega}_{(s)/\mathcal{R}}

D’après l’étude des systèmes en rotation on en déduit :

\begin{matrix} \lVert \overrightarrow{v}_{A\in (s)/\mathcal{R}} \rVert =\overrightarrow{\Omega}_{(s)/\mathcal{R}}.IA \\ \lVert \overrightarrow{v}_{B\in (s)/\mathcal{R}} \rVert = \overrightarrow{\Omega}_{(s)/\mathcal{R}}.IB \\ \lVert \overrightarrow{v}_{C\in (s)/\mathcal{R}} \rVert = \overrightarrow{\Omega}_{(s)/\mathcal{R}}.IC \end{matrix}

Si on connait la vitesse de au moins deux points du solide, on peut déterminer le CIR, et en déduire la vitesse de rotation : \boxed{ \lVert \overrightarrow{\Omega}_{(s)/\mathcal{R}} \rVert = \frac{\lVert \overrightarrow{v}_{A\in (s)/\mathcal{R}} \rVert }{IA} = \frac{\lVert \overrightarrow{v}_{B\in (s)/\mathcal{R}} \rVert }{IB} = \frac{\lVert \overrightarrow{v}_{C\in (s)/\mathcal{R}} \rVert }{IC} }

Pour mémoriser facilement les relations, on peut simplifier l’écriture ci-dessus en notant V_A = \lVert \overrightarrow{v}_{A\in (s)/\mathcal{R}} \rVert et \Omega = \lVert \overrightarrow{\Omega}_{(s)/\mathcal{R}} \rVert :

\text{si $I$ est le CIR et } A \in (s) \text{ alors } \boxed{ V_A = IA.\Omega } \Longleftrightarrow \boxed{ \Omega = \frac{V_A}{IA} }

Remarque: On retrouve la propriété de la vitesse de translation d’un point en rotation autour d’un axe fixe: le module de la vitesse est égal au rayon multiplié par la vitesse de rotation

---

4 Mouvements d’un ensemble de solides

On considère 3 solides (1), (2), et (3) en mouvement

to do : ajouter figure et animation 

4.1 Composition des vitesses

Les vitesses et vitesses de rotation des solides (1), (2), et (3) sont liées ainsi:

\boxed{ \overrightarrow{v}_{A\in(1)/(3)} = \overrightarrow{v}_{A\in(1)/(2)}+\overrightarrow{v}_{A\in(2)/(3)} }

\boxed{ \overrightarrow{\Omega}_{(1)/(3)} = \overrightarrow{\Omega}_{(1)/(2)}+\overrightarrow{\Omega}_{(2)/(3)} }

Soit, sous la forme de somme de torseurs cinématiques :

\boxed{ \Big\{ \mathcal{V}_{(1)/(3)} \Big\}_A = \Big\{ \mathcal{V}_{(1)/(2)} \Big\}_A + \Big\{ \mathcal{V}_{(2)/(3)} \Big\}_A }

Pour mémoriser ces relations : il faut remarquer qu’elles ont la forme d’une relation de Chasles

Exemple: une personne se déplace dans un train (mouvement horizontal), et lance verticalement un objet \Longrightarrow les vaches dans le champ observent que l’objet a une trajectoire oblique (combinaison de la vitesse relative de l’objet par rapport au train et de la vitesse du train par rapportt au sol).

---

4.2 Propriétés des CIR

Si 3 solides (1), (2), et (3) sont en mouvement les uns par rapport aux autres, alors :

• Les 3 CIR relatifs I_{1/2}, I_{2/3}, I_{1/3} sont alignés

• Le rapport des vitesses de rotation est égal au rapport des distances entre les CIR :

\boxed{\frac{\Omega_{2/1}}{\Omega_{3/2}}=\frac{I_{2/3}I_{3/1}}{I_{3/1}I_{1/2}}}

• On en déduit: \boxed{\frac{\Omega_{3/1}}{I_{3/2}I_{2/1}}=\frac{\Omega_{2/1}}{I_{2/3}I_{3/1}}=\frac{\Omega_{3/2}}{I_{3/1}I_{1/2}}}

    to do : ajouter figures + lien vers système bielle manivelle 

---

5 Champ des accélérations d’un solide

On considère un solide (s) en mouvement par rapport à un référentiel \mathcal{R}, et A et B deux points du solide.

Pour déterminer l’accélération de B, on dérive la vitesse de B par rapport au temps: \overrightarrow{\Gamma}_{B\in (s)/\mathcal{R}}=\dot{\vec{v}}_{B\in (s)/\mathcal{R}}

Nous avons déterminé que si on connait la vitesse \vec{v}_A et le vecteur rotation \overrightarrow{\Omega}_{(s)/\mathcal{R}}, la vitesse de B peut être déterminée par la relation suivante: \vec{v}_{B\in (s)/\mathcal{R}} = \vec{v}_{A\in (s)/\mathcal{R}} + \overrightarrow{BA} \wedge \overrightarrow{\Omega}_{(s)/\mathcal{R}}

Pour déterminer l’accélération de B en fonction de l’accélération de A, on dérive l’expression précédente par rapport à t : \overrightarrow{\Gamma}_{B\in (s)/\mathcal{R}} = \dot{\overrightarrow{v}}_{B\in (s)/\mathcal{R}} + \dot{\overrightarrow{BA}} \wedge \overrightarrow{\Omega}_{(s)/\mathcal{R}} + \overrightarrow{BA} \wedge \dot{\overrightarrow{\Omega}}_{(s)/\mathcal{R}}

• \dot{\overrightarrow{v}}_{B\in (s)/\mathcal{R}} est l’accélération \overrightarrow{\Gamma}_{B\in (s)/\mathcal{R}}

• La distance BA est constante car A et B \in \ (s), mais la direction de \overrightarrow{BA} n’est pas constante si \overrightarrow{\Omega}_{(s)/\mathcal{R}} \ \neq \ \vec{0}

  \overrightarrow{BA}=\overrightarrow{BO}+\overrightarrow{OA}, donc : \dot{\overrightarrow{BA}}=\dot{\overrightarrow{BO}}+\dot{\overrightarrow{OA}} soit: \dot{\overrightarrow{BA}} = -\vec{v}_{B\in (s)/\mathcal{R}} + \vec{v}_{A\in (s)/\mathcal{R}} D’après la relation \vec{v}_{B\in (s)/\mathcal{R}} = \vec{v}_{A\in (s)/\mathcal{R}} + \overrightarrow{BA} \wedge \overrightarrow{\Omega}_{(s)/\mathcal{R}} on peut écrire : \dot{\overrightarrow{BA}} = \vec{v}_{A\in (s)/\mathcal{R}}-\vec{v}_{B\in (s)/\mathcal{R}} = -\overrightarrow{BA} \wedge \overrightarrow{\Omega}_{(s)/\mathcal{R}}

• On en déduit:

  \overrightarrow{\Gamma}_{B\in (s)/\mathcal{R}} = \overrightarrow{\Gamma}_{A\in (s)/\mathcal{R}} + (-\overrightarrow{BA} \wedge \overrightarrow{\Omega}_{(s)/\mathcal{R}}) \wedge \overrightarrow{\Omega}_{(s)/\mathcal{R}} + \overrightarrow{BA} \wedge \dot{\overrightarrow{\Omega}}_{(s)/\mathcal{R}}

  En introduisant l’accélération angulaire \boxed{\overrightarrow{\alpha}_{(s)/\mathcal{R}}=\dot{\overrightarrow{\Omega}}_{(s)/\mathcal{R}}}
  et en inversant l’ordre du double produit vectoriel, et en réorganisant l’ordre des termes, on obtient finalement:
  \boxed{ \overrightarrow{\Gamma}_{B\in (s)/\mathcal{R}} = \overrightarrow{\Gamma}_{A\in (s)/\mathcal{R}} + \overrightarrow{BA} \wedge \overrightarrow{\alpha}_{(s)/\mathcal{R}} + \overrightarrow{\Omega}_{(s)/\mathcal{R}} \wedge (\overrightarrow{BA} \wedge \overrightarrow{\Omega}_{(s)/\mathcal{R}}) }

  \Longrightarrow Si on connait l’accélération d’un point A du solide (S) et le vecteur rotation \overrightarrow{\Omega}_S, alors on peut déterminer l’accélération de tous les points du solide.

  Ce qu’il faut remarquer c’est que l’on ne retrouve pas d’expression similaire à la formule de Varignon, il y a un terme supplémentaire. En conséquence, l’accélération n’a pas les propriétés d’un champ de vecteurs équiprojectifs, et donc contrairement à la vitesse, on ne peut pas écrire un torseur des accélérations

  A RETENIR : il n’y a pas de torseur des accélérations

---

A retenir :

• La vitesse de glissement:

\boxed{ \overrightarrow{v}_{I\in (2)/(1)} = \overrightarrow{v}_{I\in (2)/\mathcal{R}} - \overrightarrow{v}_{I\in (2)/\mathcal{R}} }

• CIR :

  • le CIR I est situé à l’intersection des perpendiculaires au vecteurs vitesse
  • \boxed{ \lVert \overrightarrow{\Omega}_{(s)/\mathcal{R}} \rVert = \frac{\lVert \overrightarrow{v}_{A\in (s)/\mathcal{R}} \rVert }{IA} }
  • \boxed{ \frac{\lVert \overrightarrow{v}_{A\in (s)/\mathcal{R}} \rVert }{IA} . \lVert \overrightarrow{\Omega}_{(s)/\mathcal{R}} \rVert}

---

5.0.1 Applications

voir TD

• Glissement d’une échelle

• Joint de cardan

• Mouvement d’une benne

• Roulement sur un plan

• crémaillère

• Engrenages

• Roulements

5.1 Accélération

6 Mouvement de référentiels

a compléter