RAPPELS

1 A revoir (pré-requis) :

• cours de mécanique du BUT 1

  • vecteurs, coordonnées
  • actions mécanique
  • degrés dee liberté, degrés de liaison

• cours de mécanique du S3

  • cinématique et dynamique du point
  • dérivées, systèmes dee coordonnées polaires et cylindriques
    • cylindrique
  • systèmes oscillants

• Cours de Maths

  • dérivation et intégration
  • trigonométrie
    
  • opérations sur les vecteurs
    • produit scalaire
    • produit vectoriel
    • norme
  • équations différentielles (du 1er et du 2ème ordre à coefficients constants avec ou sans second membre)
    
  • résolution de systèmes d’équations

2 Référentiels, repères

• Notion de référentiel \mathcal{R}

• Systèmes de coordonnées

• Cartésiennes

• Polaires

• Cylndriques

• Vecteur position d’un point dans l’espace \overrightarrow{OP}

• Vecteur Vitesse d’un point

\overrightarrow{v_P}=\frac{\rm{d}\overrightarrow{OP}}{\rm{d}t}

• Vecteur accélération d’un point \overrightarrow{\Gamma_P}=\frac{\rm{d}\overrightarrow{OP}}{\rm{d}t}

• dérivation des vecteurs vitesse et accélération définis avec des vecteurs de base mobile

En coordonnées polaires :

• $ = … $

REVOIR LE S3

3 Moments des forces

3.1 Définition

Soit une force \ovrrightarrow{F} appliqué en un point B.

Le moment …

3.2 Approche géométrique

• Schéma avec bras de levier

• Formule module

3.3 Propriétés

AB,F perp M

module

trièdre direct

3.4 Formule de Varignon

4 Torseur des actions mécaniques

• moment résultant

4.1 Forces, Moments

Les actions mécaniques peuvent êtres décrites par deux types de grandeurs : Forces et moments

4.1.1 Les vecteurs forces

Permettent de modéliser la capacité d’une action à produire une translation

Les directions et sens d’un vecteur force indique la direction et le sens de la translation que l’action mécanique a tendance à produire.

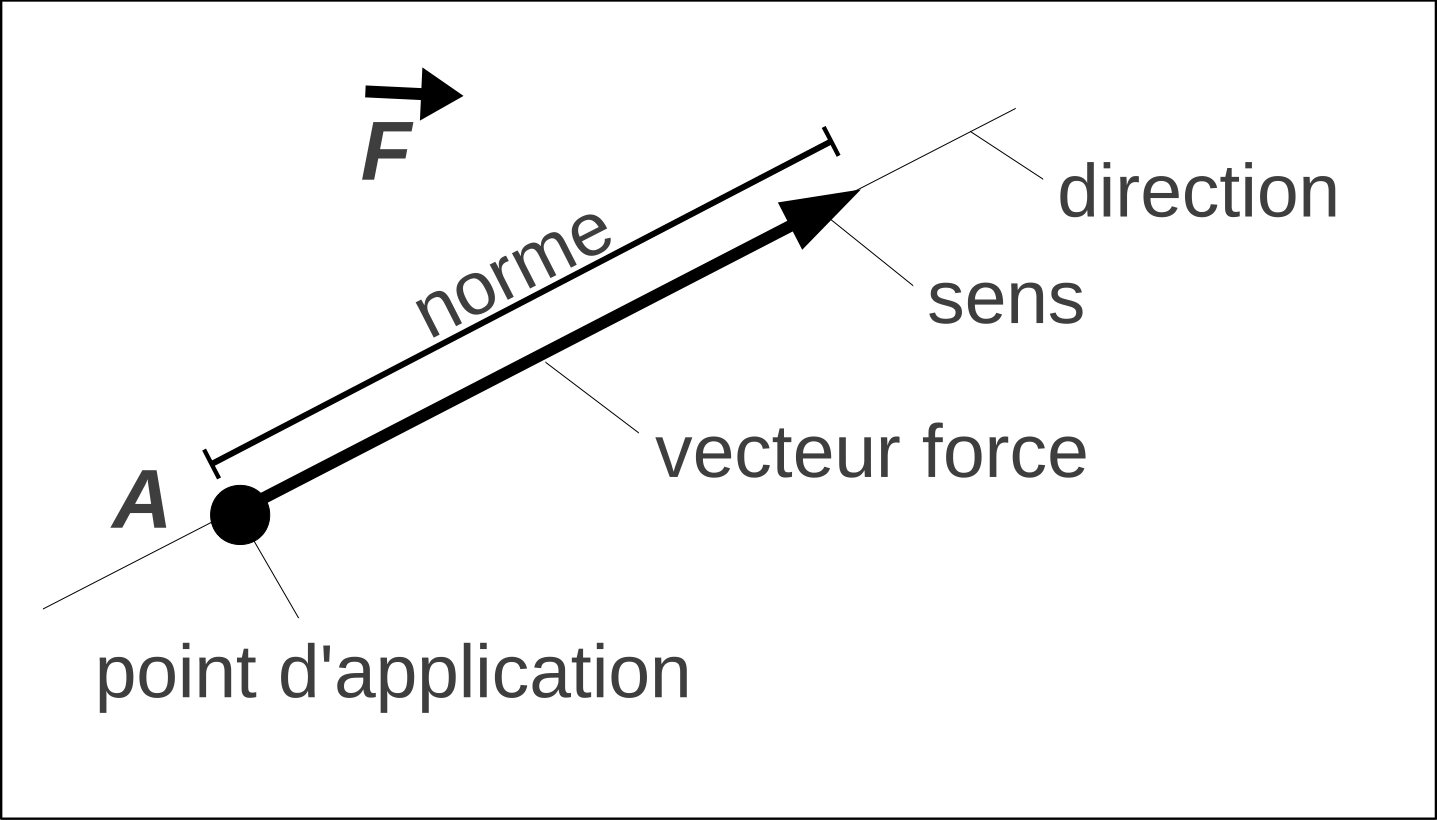
Exemples:
le poids, la force de rappel exercée par un ressort, la tension d’un cable, la poussée d’un vérin, une force de frottement, une force électrostatique, la réaction d’un support ou d’un axe, …

la résultante des forces est la somme des forces appliquée à un solide.

ATTENTION: Traiter les forces comme des vecteurs et pas comme des nombres !!!

4.1.2 Les vecteurs moments

Permettent de modéliser la capacité d’une action à produire une rotation

La direction d’un moment en un point P indique la direction de l’axe de rotation passant par P autour duquel l’action à tendance à faire tourner.

Toute force exerce un moment si le point d’application n’appartient pas à la droite qui porte le vecteur force

Les moteurs sont conçus pour exercer un moment, les eengrenages sont des éléments permettant de transmettre un moment

Les moments appliqués à un solide peuvent être calculés par rapport à un point unique afin de calculer leur somme, le moment résultant

insérer schémas

4.2 Le torseur des actions mécaniques

Le torseur des actions mécanique permet de regrouper le vecteur force et le vecteur moment :

recopier la formule

Pour détreminer le torseur des actions appliquées à un solide isolé (s), il faut établir le bilan des actions mécaniques extérieures et rassembler les informations suivantes pour chacune des actions :

Nom	symbole de la force	point d’application	coordonnées du vecteur force	symbole du moment	coordonnées du moment

4.2.1 Exemple

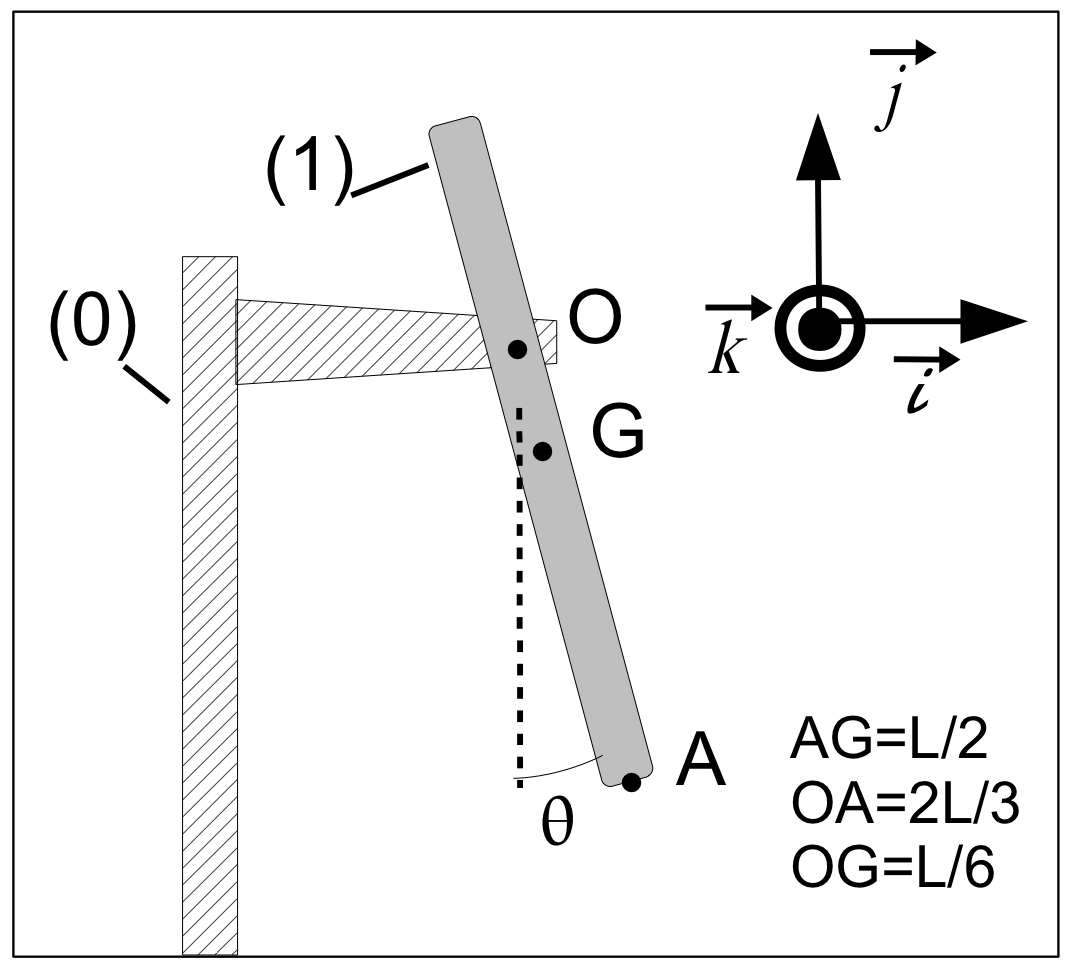
Question: déterminer le torseur des actions mécaniques réduit au point O dans le cas où on néglige les frottements au niveau de l’axe.

Bilan des actions mécaniques extérieures (BAME):

Nom	symbole de la force	point d’application	coordonnées du vecteur force	symbole du moment / O	coordonnées du moment
Poids	\overrightarrow{P}	G	\begin{pmatrix} 0 \\ -m g \\ 0 \end{pmatrix}	\overrightarrow{\mathcal{M}}_{\vec{P}/O}	\begin{pmatrix} 0 \\ 0 \\ -m g L \sin{(\theta ) / 6} \end{pmatrix}
Réaction de l’axe	\overrightarrow{R}_{(0) \rightarrow (1)}	O	\begin{pmatrix} R_x \\ R_y \\ 0 \end{pmatrix}	\overrightarrow{\mathcal{M}}_{\vec{R}_{(0)\rightarrow (1)}/O}	\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}

Du BAME, on déduit les éléments du torseur des actions mécaniques extérieures appliquées sur le solide :

• La résultante (forces) : \begin{pmatrix} R_x \\ R_y-m g \\ 0 \end{pmatrix}

• Le moment au point O: \begin{pmatrix} 0 \\ 0 \\ -m g L \sin{(\theta ) / 6} \end{pmatrix}

• Le torseur des actions mécaniques

  \boxed{ \ \left\{ \mathcal{A}\right\}_{O} = \begin{Bmatrix} R_x & 0 \\ R_y-m g & 0 \\ 0 & -m g L \sin(\theta ) / 6 \end{Bmatrix}_{O} \ }