Glissement d’une échelle
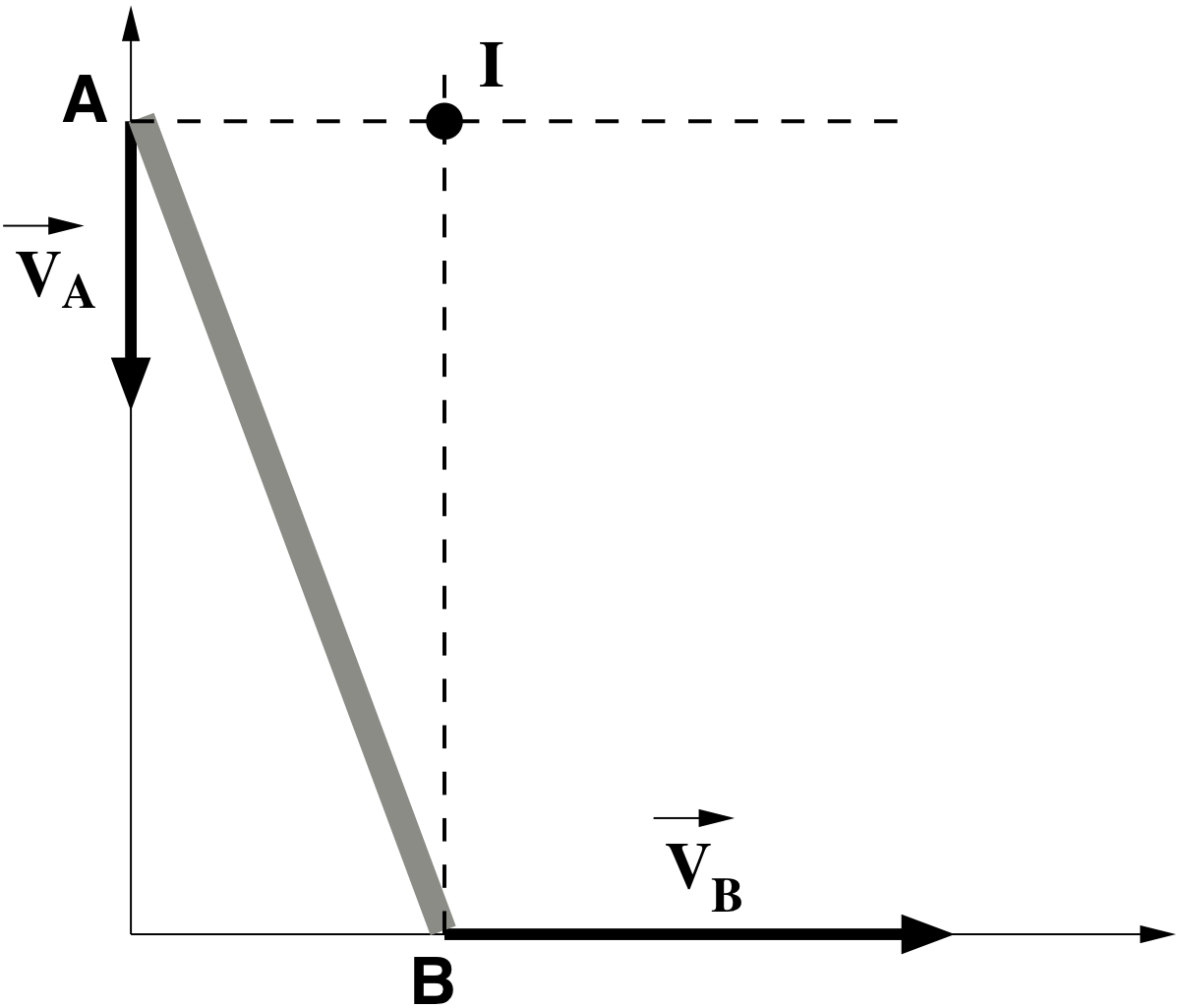
On étudie le mouvement d’une échelle qui glisse. On souhaite notamment déterminer la vitesse du point B et le vecteur rotation en utilisant l’équiprojectivité et/ou le centre instantanné de rotation (CIR).
Données
Echelle de longueur AB=3 m
L’échelle est en mouvement (glisssement). Le mouvement est plan.
On appelle Ox l’axe défini par le sol, et Oy celui défini par le mur vertical. On y associe les vecteurs unitaires \vec{i} et \vec{j}
A l’instant correspondant à la position “photographiée” sur le schéma: \overrightarrow{v}_A = -0.5 \vec{j}, \theta=30^\circ.
Questions
Que vaut la vitesse de rotation \overrightarrow{\Omega} ?
Que vaut la vitesse \overrightarrow{v_B} ?
Résolution en un utilisant l’équiprojectivité
Résolution en un utilisant les propriétés du CIR
On détermine la position du CIR, que l’on appelle I :
IA \perp \overrightarrow{v}_A & IB \perp \overrightarrow{v}_B \Longrightarrow le CIR I est situé à l’intersection de IA et IB (voir le schéma).
On en déduit ses coordonnées:
- x_I=AI=AB.\sin(30^\mathrm{o})=1.5 m
- y_I=BI=AB.\cos(30^\mathrm{o})=2.6 m
On en déduit ensuite la vitesse de rotation d’après les ppropriétés du CiR : \boxed{\Omega = v_A/IA = 0.33 \rm{rad/s} }
- Finalement on détermine v_B = IB.\Omega = 0.866 \rm{rad/s} \ \Longrightarrow \ \boxed{ \Longrightarrow \vec{v}_B=0.866 \vec{i} }