BUT GIM - Semestre 3
Avertissements:
Ce qui suit n’a pas la prétention d’être un cours complet et exhaustif conccernant la numérisation du signal. L’ambition est d’introduire smplement quelques notions élémentaires concernant les propriétés des signaux numériques. Cela passe par certaines simplifications pour aller à l’essentiel en 1ère approche.
Les aspects technologiques, matériels, composants, algorithmiques, etc., ne sont pas abordés. On se concentre sur les différences entre les signaux analogiques et les signaux numériques.
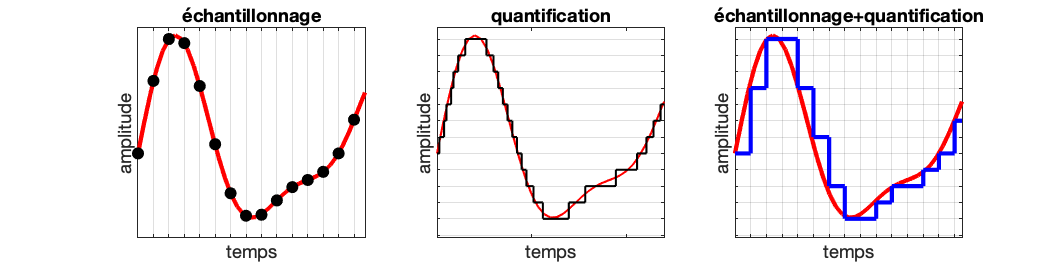
l’échantillonnage prélève, le plus souvent à intervalles réguliers, la valeur du signal ;
la quantification transforme une valeur quelconque en une valeur prise dans une liste finie de valeurs valides pour le système ;
le codage fait correspondre à chaque valeur valide pour le système un code numérique.
La période d’échantillonnage à laquelle les valeurs du signal sont prélevées est fixée par le choix de la fréquence d’échantillonnage [eng: sampling frequency ou sampling rate].
La quantification permet d’approcher par un ensemble de valeurs discrètes l’amplitude d’un signal continu.

Légende:
* trait rouge: signal analogique s(t)
* à gauche : échantillonnage à intervalles réguliers. Points noirs : valeurs du signal écchantillonnées à des instants distants de \Delta t = 1/ F_e, avec F_e la fréquence d’échantillonnage.
* au milieu : on approche les valeurs continues du signal analogique par des valeurs prédéfines par le système d’acquisition et son réglage \longrightarrow trait noir
* à droite : en bleu, le résultat de la combinaison des deux opérations (signal bleu: rendu sous forme d’échantillonnage-blocage [wikipeddia])
L’erreur de quantification apparait lorsqu’il y a une conversion analogique-numérique du signal
Les valeurs sont échantillonnées à intervalle de temps (le plus souvent régulier), déterminé par la fréquence d’échantillonnnage.
L’amplitude d’un signal analogique s(t) est codée selon des valeurs numériques discrètes dont le pas \Delta s dépend du nombre de bits sur lequel l’amplitude est codée (codage sur 8 bits : 2^8 = 256 valeurs possibles, codage sur 12 bits : 2^{12} = 4096 valeurs possibles).
Par exemple : pour une carte d’acquisition dont le calibre d’entrée est \pm 10 Volts, le pas de quantification pour un codage sur 8 bits est 78,4 mV, tandis qu’il est de 4.9 mV pour un codage sur 12 bits. L’incertitude maximale liée à la quantification d’un signal s(t) est de \pm\Delta s.
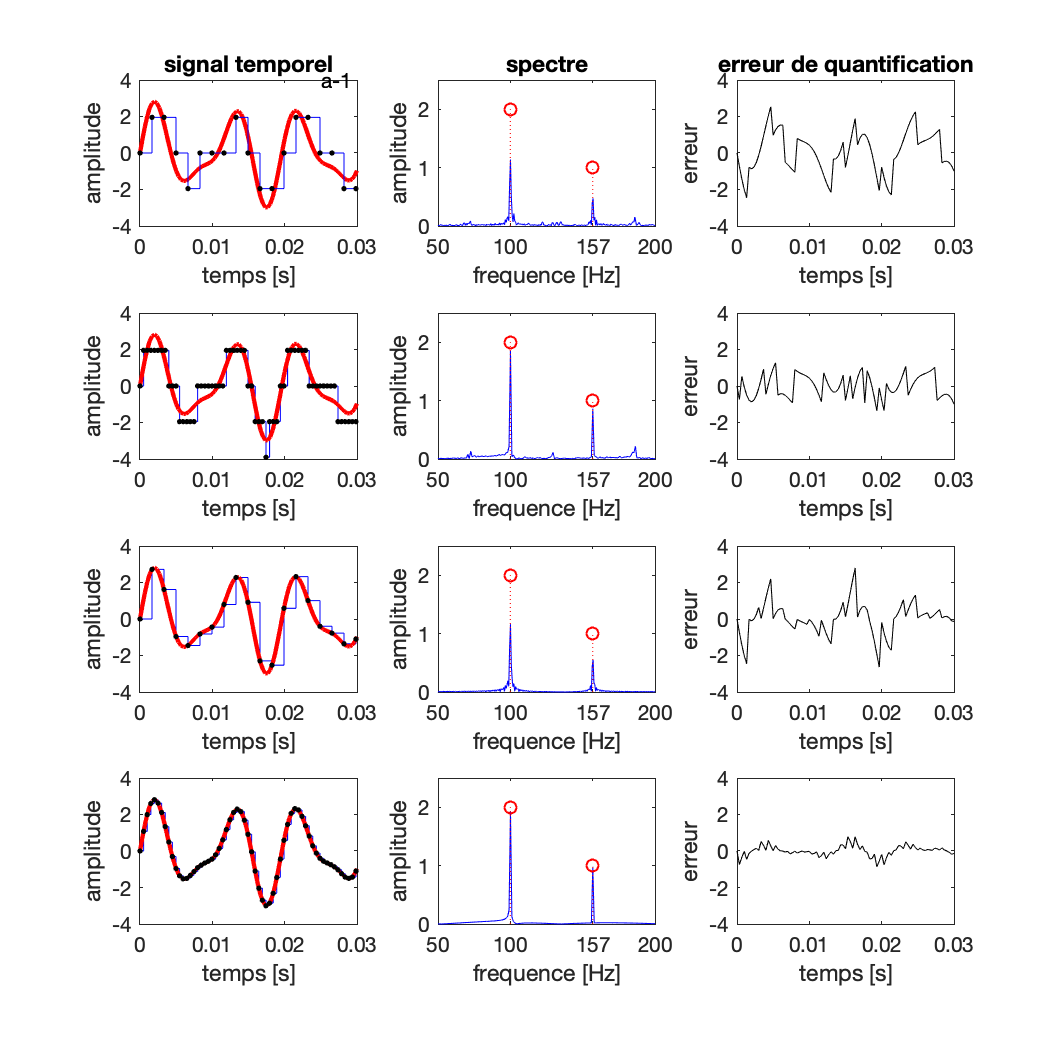
Légende :
Acquisition numérique et analyse spectrale d’un signal constitué de deux composantes sinusoidales :
s(t)= A_1 \sin (2 \pi F_1 t) + A_2 \sin (2 \pi F_2 t)
avec A_1=2, A_2=1, F_1=100 Hz, et F_2=157 Hz
Figures :
de haut en bas : différents paramètres de numérisation : \Delta s et Fréquence d’échantillonnage F_e (et \Delta t).
couleurs et symboles :
Commentaires :
On se concentre dans la suite, sur les domaines temporels et fréquentiels
Fréquence d’échantillonnage F_s : fréquence à laquelle les valeurs du signal sont mémorisées, notées F_e dans ce cours, et souvent noté F_s pour sampling frequency ou s_r pour sampling rate
Pas d’échantilonnage \delta t : intervalle de temps entre 2 prises de valeur, \delta t = 1/F_s
Si on note t_n les valeurs discrètes du temps, alors : \delta t = t_{n+1}-t_n
On s’apperçoit facilement que la fréquence d’échantillonnage doit être nettement plus élevée que les fréquences des phénomènes que l’on analyse
Dans la suite on s’intéresse plus en détail à l’influence des paramètres d’échantillonnages sur l’analyse des fréquences.
Avertissement :
On se limite à introduire les notions élémentaires pour une prermière approche, en lien avec l’acquisition numérique du signal. L’ambition n’est pas d’être complet ni exhaustif.
L’analyse spectrale consiste à analyser le contenu fréquentiel d’un signal.
Pour sensibiliser les principes et l’intérêt de l’analyse des fréquences qui constituent les signaux alternatifs, considérons d’abord le cas du signal ci-dessous, représenté en fonction du temps comme on pourrait le visualiser sur un oscilloscope :
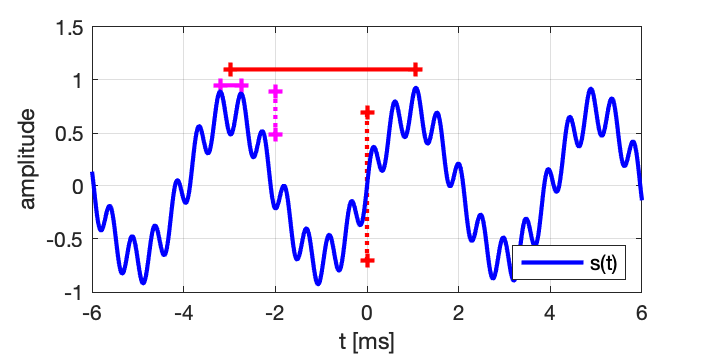
Remarque :
Comme nous percevons mieux les fréquences élevées que les fréquences graves, malgré la différence d’amplitude que l’on peut observe, le signal de fréquence élevée nous appparaît, à l’écoute, à peu près du même niveau que la basse fréquence.
Cette sensation déppend aussi du système d’écoute (haut-parleurs, casque) et de l’appareil (ordinateur ou tablette, smartphone).
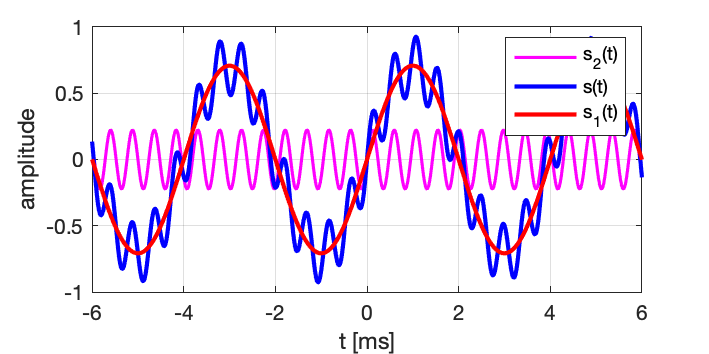
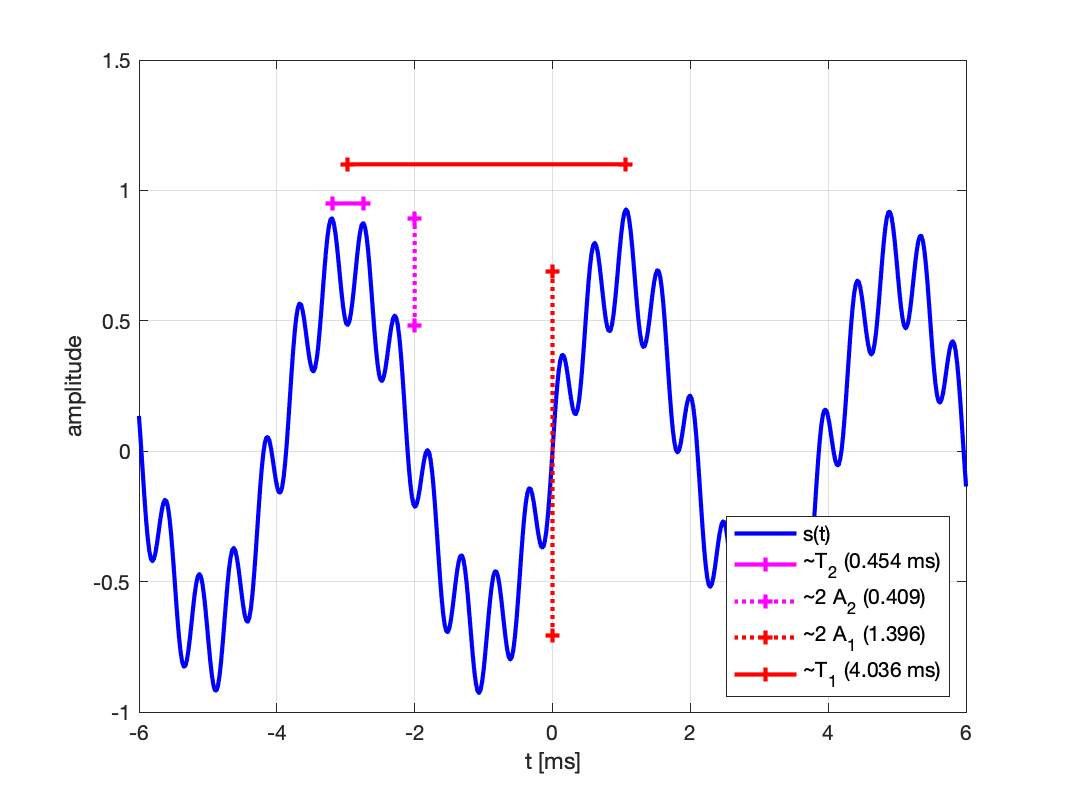
On en déduit des valeurs approchées des amplitudes et des fréquences :
\tilde{F_1}=248 Hz (valeur exacte F_1 = 250 Hz) ;
\tilde{F_2}=2205 Hz (valeur exacte F_2 = 2100 Hz) ;
\tilde{A_1}=0.698 (valeur exacte A_1 = 0.708) ;
\tilde{A_2}=0.205 (valeur exacte A_2 = 0.224 ).
On peut alors réduire l’information et représenter le signal sous la forme d’une courbe représentant l’amplitude en fonction de la fréquence :
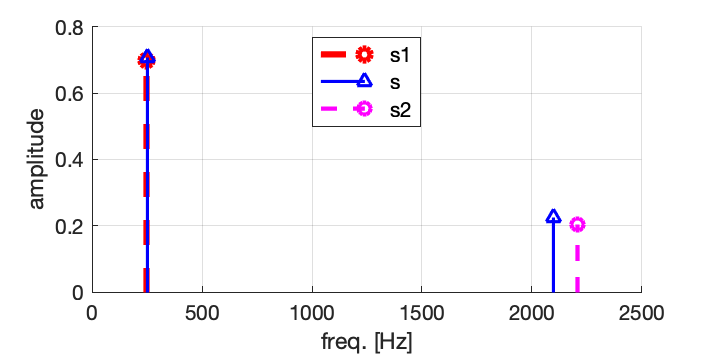
Ce type de représentation, l’amplitude en fonction de la fréquence, est le spectre du signal.
Dans de nombreuses applications, et notamment en acoustique, vibrations, audio, électronique, etc, on représente souvent les amplitudes en échelle logarithmique, et notamment en décibels.
Si on choisit arbitrairement la valeur 1 comme référence, on peut représenter l’amplitude A du signal en \mathrm{dB}_{ref \ 1} en calculant la valeur en décibels 20 \log\left( A / 1 \right) :
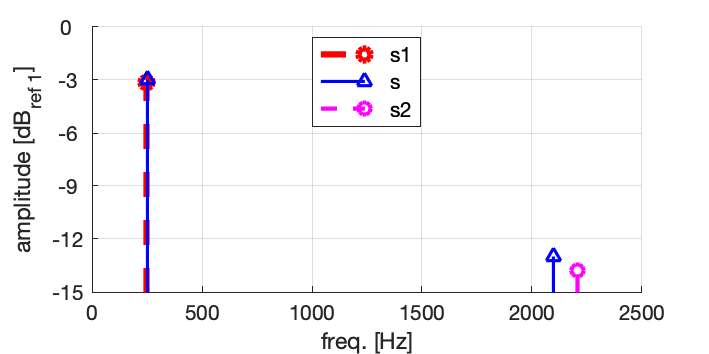
Remarque : En pratique, on utilisera des valeurs de références standard pour les dB selon la nature du signal. Par exemple: 1 Volt ou 1 microVolt, efficace, 1 Watt, 20 microPascals, 1 g, 1 \mathrm{m}/\mathrm{s}^2, etc.
L’exemple simple que nous venons de discuter en détails permet de comprendre que l’on peut analyser et représenter un signal en fonction de la fréquence (représentation spectrale, ou simplement spectre) au lieu d’une représentation temporelle (ou forme d’onde).
Mais pour des signaux plus complexes l’analyse ne peut pas se faire aussi simplement et il faut utiliser des outils plus spécifiques.
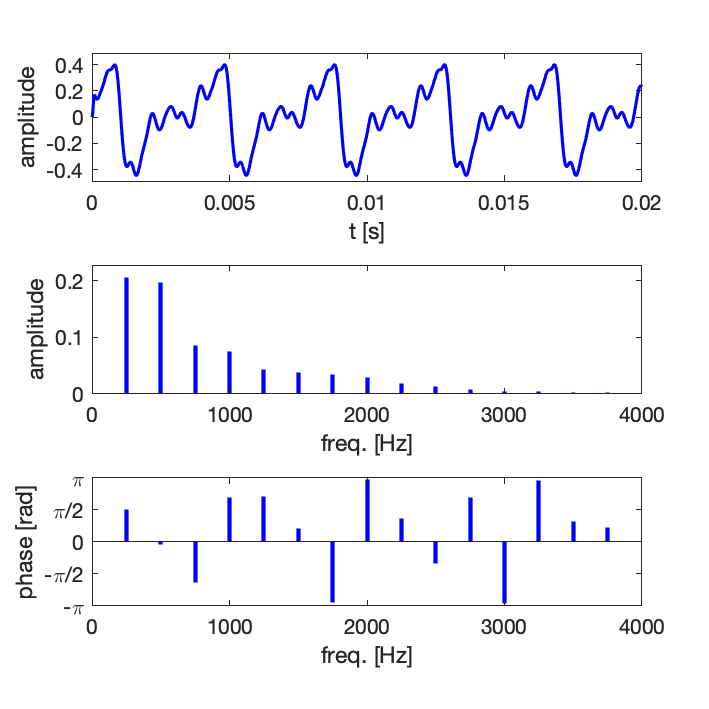
Par exemple, en écoutant le signal ci-dessous, qui contient 5 fréquences superposées, l’analyse est difficile, voire impossible, à partir du signal temporelle, ou même à l’écoute .

Considérons un signal constitué de la somme de 2 composantes sinusoïdales
où A_1 et A_2 sont les ampltudes, F_1 et F_2 les fréquences, et \phi_1 et \phi_2 les phases par rapport à une référence commune.
Le signal et ses composantes sont représentées ci-dessous en fonction du temps, ainsi qu’en fonction de la fréquence en traçant l’amplitude et la phase des composantes :
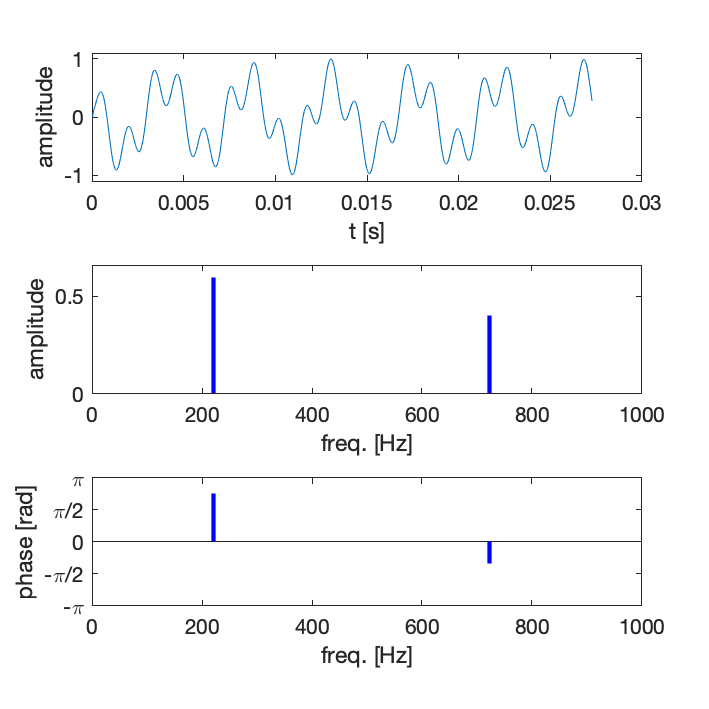
Remarques :
La phase est parfois un paramètre parfois très important, et parfois non.
Très souvent on représente uniquement l’amplitude en échelle logarithmique par rapport à une référence, sans préciser la phase.
En pratique, on représente souvent en amplitude la valeur efficace, ou bien la puissance, ou la densité spectrale de puissance, et très souvent en échelle logarithmique.
Analyse / Synthese
pour représenter le spectre d’un signal, il faut d’abord savoir l’analyser et extraire les paramètres de chaque composante fréquentielle.
L’analyse fréquentielle vise à évaluer les amplitudes et éventuellement la phase des différentes composantes fréquentielles
On parle de synthèse lorsque l’on reconstitue le signal en sommant les différentes composante. (En musique, la synthèse sonore par addition de composantes sinusoïdales est appelée “synthèse additive”)
L’analyse des fréquences des signaux périodiques est vue en cours de mathématiques dans le cours sur les séries de Fourier.
l’analyse spectrale est appelée analyse de Fourier en référence au Mathématicien et Physicien Joseph Fourier wikipedia
Sans développer un cours de mathématiques ici, on présente ci-dessous quelques élément sur la décomposition en séries de Fourier
Les signaux périodiques sont constitués de composantes dites harmoniques, c’est-à-dire telles que les fréquences F_{nh} des différentes composantes du signal ont des fréquences liées à une fréquence fondamentale F_0 de la manière suivante :
F_{nh} = n F_0, \ \ \text{avec} \ \ n= 1, 2, 3, 4, ...
Remarque : toutes les composantes n ne sont pas forcément présentes dans le signal, ou, autrement dit, certaines peuvent avoir une amplitude A_n nulle. La fondamentale peut également avoir une amplitude nulle.
exemple_signal_periodique_serie_Fourier.mp3
Avertissements :
On aborde souvent la décomposition de signaux périodiques s(t) sous la forme de séries du type
S_n (t) = a_0 + \sum_{n=0}^{n=N} a_n \sin(n \omega_0 t) + \sum_{n=0}^{n=N} b_n \sin(n \omega_0 t) où :
n = 1, 2, 3..., a_0, a_n, et b_n sont des coefficients réels;
\omega_0, f_0 = \omega_0 / (2 \pi), et T_0 = 2 \pi / \omega sont la pulsation, la fréquence, et la période fondamentales.
On peut écrire la série en faisant apparaître l’argument des fonctions sinus ou cosinus sous différentes formes : (n \omega_0 t) ou ( 2 \pi n f_0 t), ou encore (n 2 \pi t / T_0 ).
On trouve aussi des formes où l’on fait apparaître \omega_n = n \omega_0, f_n = n f_0.
Les coefficients a_0, a_n, et b_n se déterminent comme ceci :
le coefficient a_0 correspond à la composante ontinue du signal (sa moyenne sur une période) :
a_0 = \frac{1}{T_0} \int_0^{T_0} s(t) \mathrm{d}t
Les autres coefficients euvent être vus comme une projection sur une base de fonctions, de manière similaire à la décomposition de vecteurs en composantes selon des vecteurs de base.
coefficients a_n, avec n\geq 1, et f_n = n \ f_0 :
a_n = \frac{1}{T_0} \int_0^{T_0} s(t) \sin(2 \pi f_n \ t)\mathrm{d}t
coefficients b_n, avec n\geq 1, et f_n = n \ f_0 :
b_n = \frac{1}{T_0} \int_0^{T_0} s(t) \cos(2 \pi f_n \ t)\mathrm{d}t
Remarque importante : Le nombre N de composantes harmoniques à prendre en compte dépend du signal. Ce nombre eut être fini, ou infini. Lorsque le nombre de composantes n’est pas suffisant, le signal S_n(t) diffère du signal original s(t).
Exemple 1 : synthèse d’un signal de forme dent de scie avec un nombre croissant de composantes harmoniques : 5, 10, 15
Comme en pratique la série ne peut pas être infinie, on observe des oscillations résiduelles, il s’agit du phénomène de Gibbs [en savoir plus sur Wikipedia].
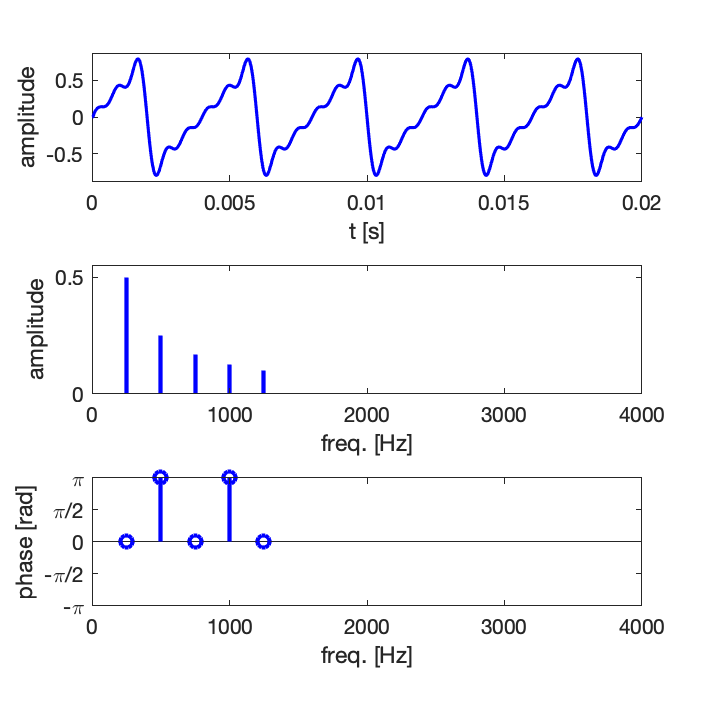
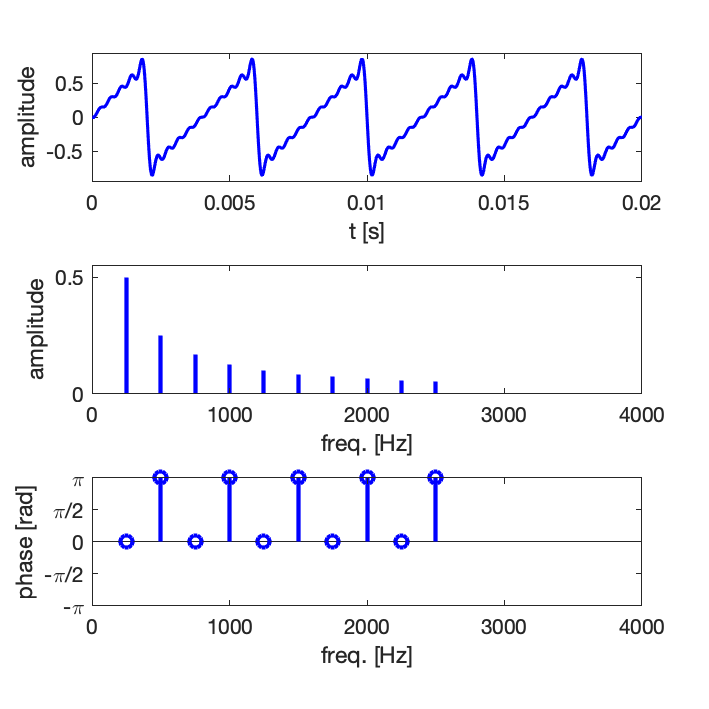
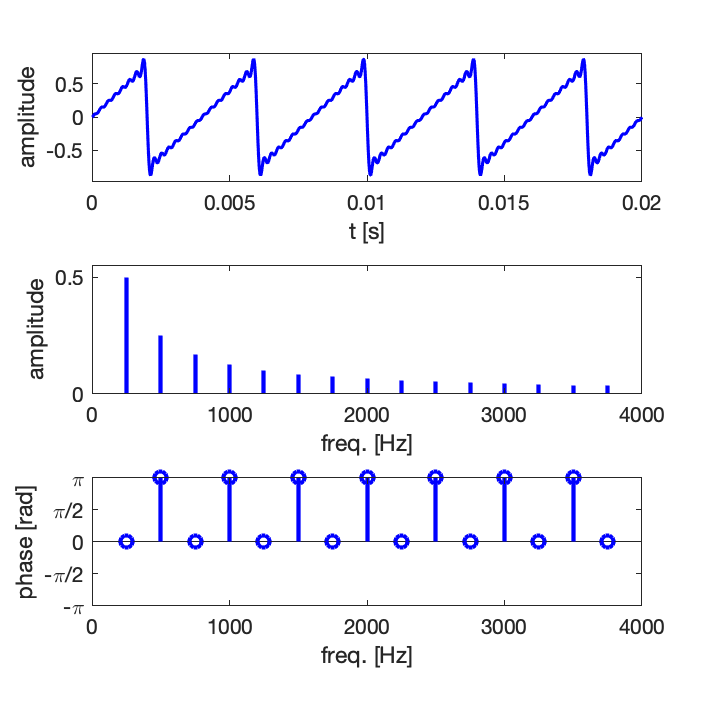
Exemple 2 : synthèse d’un signal de forme dent de scie avec un nombre croissant de composantes harmoniques : 5, 10, 15
Comme en pratique la série ne peut pas être infinie, on observe des oscillations résiduelles, il s’agit du phénomène de Gibbs [en savoir plus sur Wikipedia].
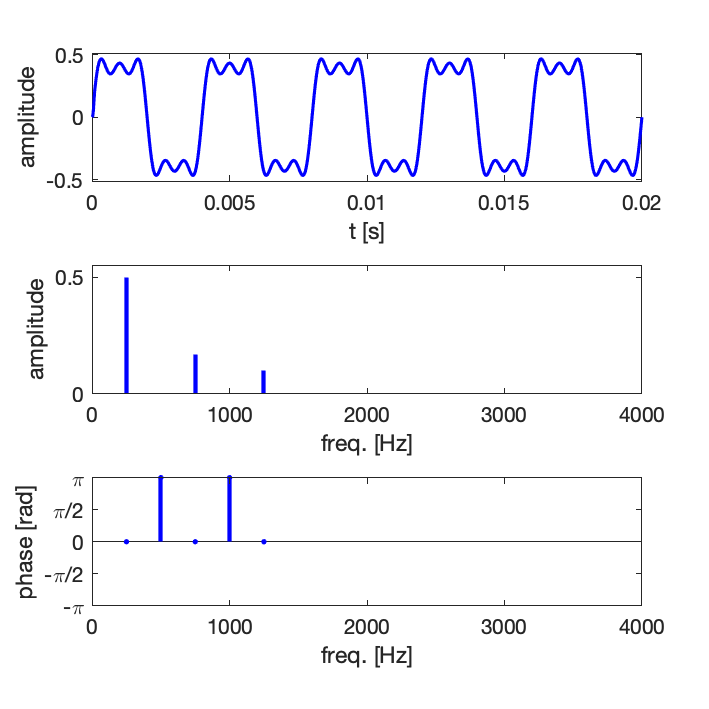
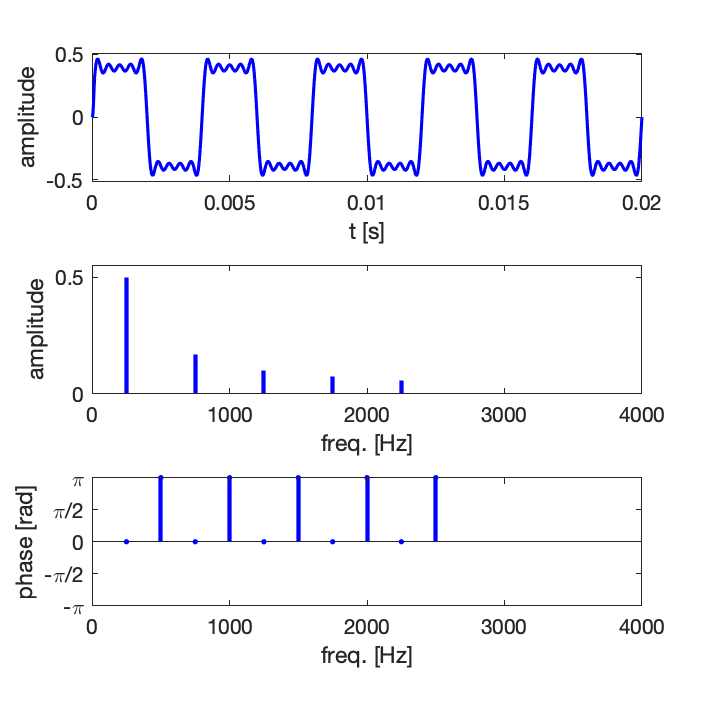
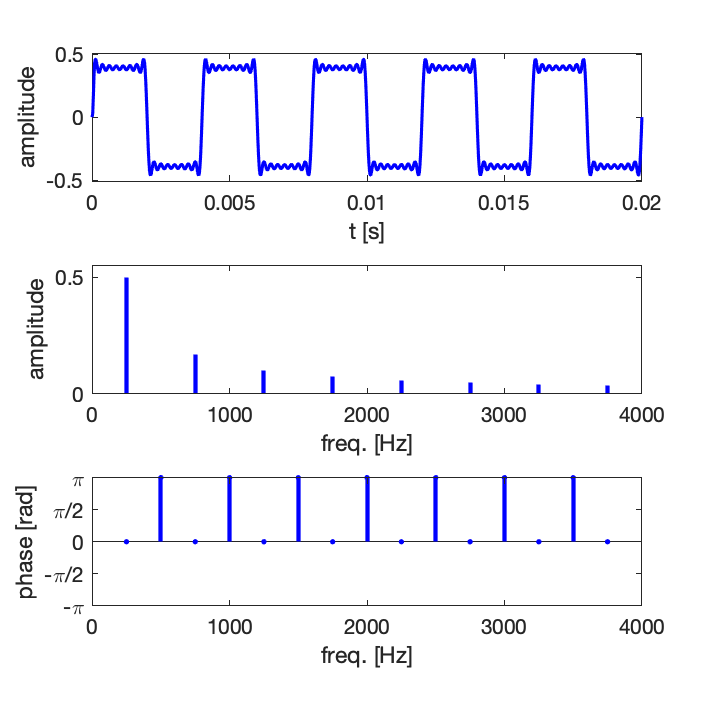
On peut aussi écrire la décomposition en série de Fourier de la manière suivante :
S_n (t) = a_0 + \sum_{n=0}^{n=N} A_n \sin(2 \pi f_n \ t + \phi_n)
ou encore
S_n (t) = a_0 + \sum_{n=0}^{n=N} A_n \cos(2 \pi f_n \ t + \psi_n)
avec f_n = n \ f_0
Les fonctions sinus et cosinus pouvant être décomposées en exponentielles, on peut aussi écrire les séries de Fourier en utilisant les fonctions exponentielles complexes :
\displaystyle S_n = \sum _{n=-\infty }^{+\infty }c_{n}{\rm {e}}^{{\rm {j}}2 \pi f_n \ t}
avec f_n = n \ f_0 (remarque : pour n=0, on retrouve a_0)
Remarque : en électricité et en physique, pour éviter la confusion avec le symbole du courant élecctrique, on préfère souvent nommer le nombre complexe \sqrt{-1} en utilisant la lettre j au lieu de la lettre i, qui est préférée en mathématiques.
En savoir plus sur wikipedia
(NB: les notations et l’ordre des explication, plus complètes et plus rigoureuses, peuvent parfois différer des choix faits ici, où l’on se contente d’une première appproche, et avec un point de vue “pratique”, notamment en privilégiant le cas des signaux réel.)
Pour des fonction (pas forcément périodiques), à support infini, la transformation de Fourier est une généralisation de l’analyse en série de Fourier des fonctions périodiques.
On peut obtenir le spectre fréquentiel S(f) d’un signal temporel s(t) en calculant la transformée de Fourier de la fonction s(t) :
\displaystyle S(f) = \int _{-\infty }^{+\infty }s(t)\,\mathrm {e} ^{-{\rm {i}}2\pi f t}\,\mathrm {d} t
Et on peut retrouver le signal temporel à partir du spectre en réalisant la Transformée de Fourier inverse
\displaystyle s(t) = \int _{-\infty }^{+\infty }S(f)\,\mathrm {e} ^{+{\rm {i}}2\pi f t}\,\mathrm {d} f
Noter le changement du signe de l’argument de l’exponentielle
Remarque : il existe des variantes dans la définition de la transformée de Fourier, différentes notamment par la valeur du coefficient de normalisation en facteur de l’intégrale, et/ou par le choix de la variable choisie pour représenter le spectre (la fréquence (f ou \nu), ou bien la pulsation \omega).
En savoir (beaucoup) plus sur wikipedia . Remarque : Dans la page Wikipedia, la fréquence est, comme souvent en physique, notée \nu (“nu”) au lieu de f.
le cours sur la Transformée de Fourier sera vu en math en BUT 3.
Avertissement: Dans ce qui suit, on ne développe pas les aspects historiques, mathématiques, ni algorithmiques. On se limite aux aspects pratiques de l’analyse fréquentielle des supports numériques, du point de vue d’un utilisateur de logiciels d’analyse ou d’appareils de mesure.
Temps discret : L’échantillonnage revient à définir le temps de manière discrète au lieu du temps continu. Cela conduit à adapter les principes développés précédemment, et définir la Transformée de Fourier des signaux Discrets.
Frequence maximum : Une des conséquences de l’échantillonnage est que l’on ne peut analyser correctement que des signaux dont la fréquence maximum est inférieure à F_e/2.
Spectre discret : Une autre conséquence est notamment que le spectre est aussi défini de manière discrète, et que l’on ne peut pas connaître le spectre de façon continue.
Durée finie : En pratique, les signaux numériques sont en pratique à support temporel fini, alors que la transformée de Fourier a été définie pour des signaux à support infini, cela a aussi des conséquences sur l’analyse des signaux.
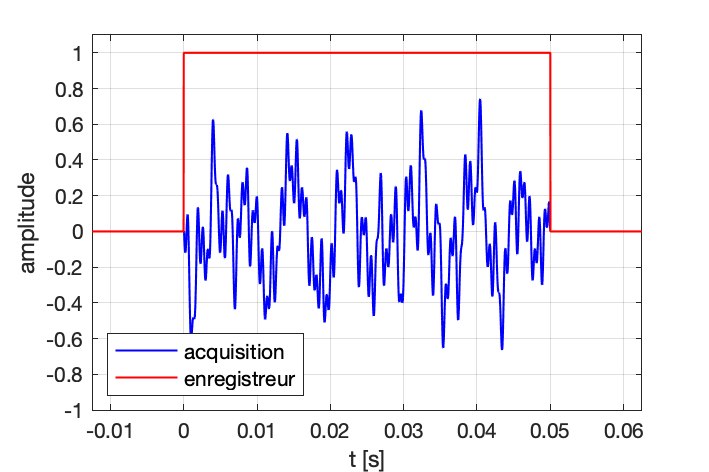
FFT : Plusieurs algorithmes permettent de calculer la transformé de Fourier discrète. Le plus couramment utilisé par les logiciels d’analyse et les apppareil de mesure est l’algorithme Fast Fourier Transform, communément appelé FFT.
On se place dans la suite dans la situation où un signal a été enregistré pendant une durée finie T, et numérisé à une fréquence d’échantillonnage Fe. On ne prête pas attention aux conséquences de la quantification (amplitude), ceci afin de se concentrer sur les aspects temporels et fréquentiels.
Le théorème de Shannon, appelé aussi Nyquist-Shannon, ou encore théorème de l’échantillonnage, énonce que l’échantillonnage d’un signal exige un nombre d’échantillons par unité de temps supérieur au double de l’écart entre les fréquences minimale et maximale qu’il contient.
En pratique, comme il est fréquent que la fréquence minimale est très inférieure à la fréquence maximale, voire qu’elle est nulle (si composante continue), on retiendra qu’il faut que la fréquence d’échantillonnage soit supérieure au double de la plus haute fréquence du signal F_{max} :
\boxed{F_e > 2 \ F_{max}}
On peut aussi dire de manière équivalente :
\boxed{F_{max} < F_e / 2 \ }
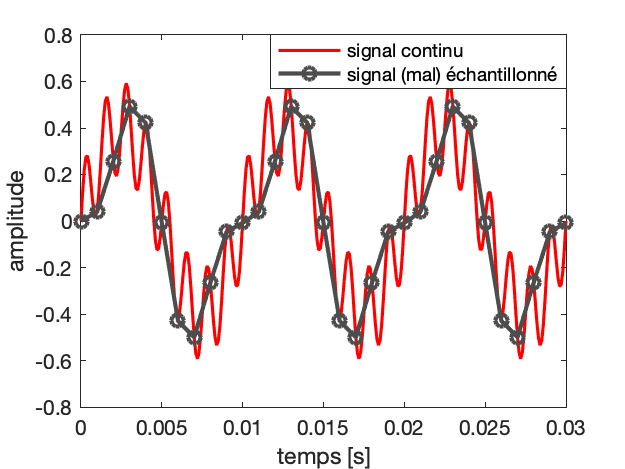
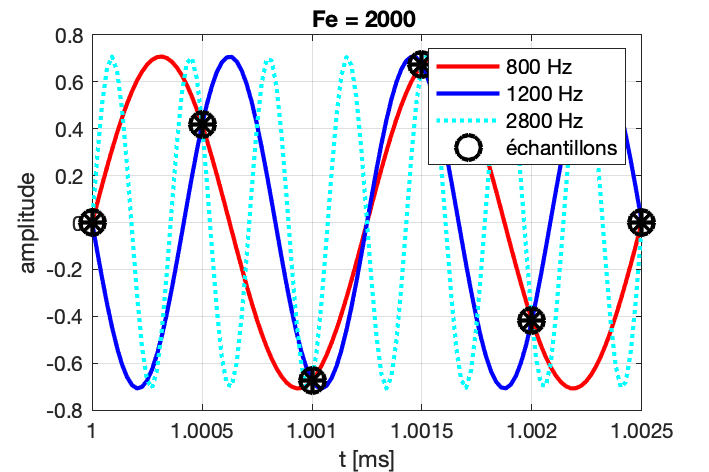
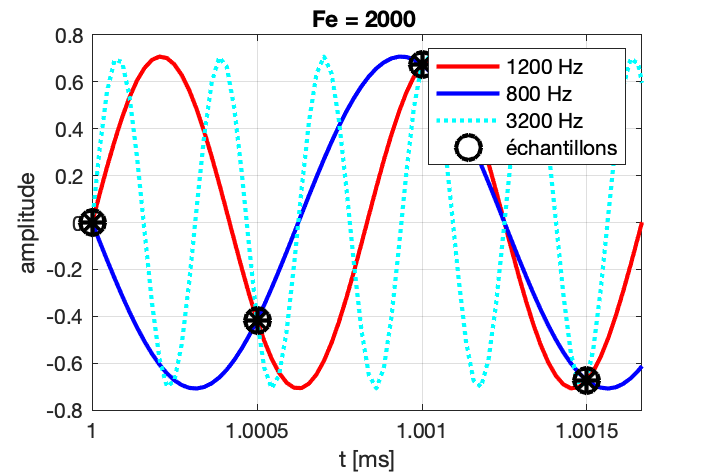
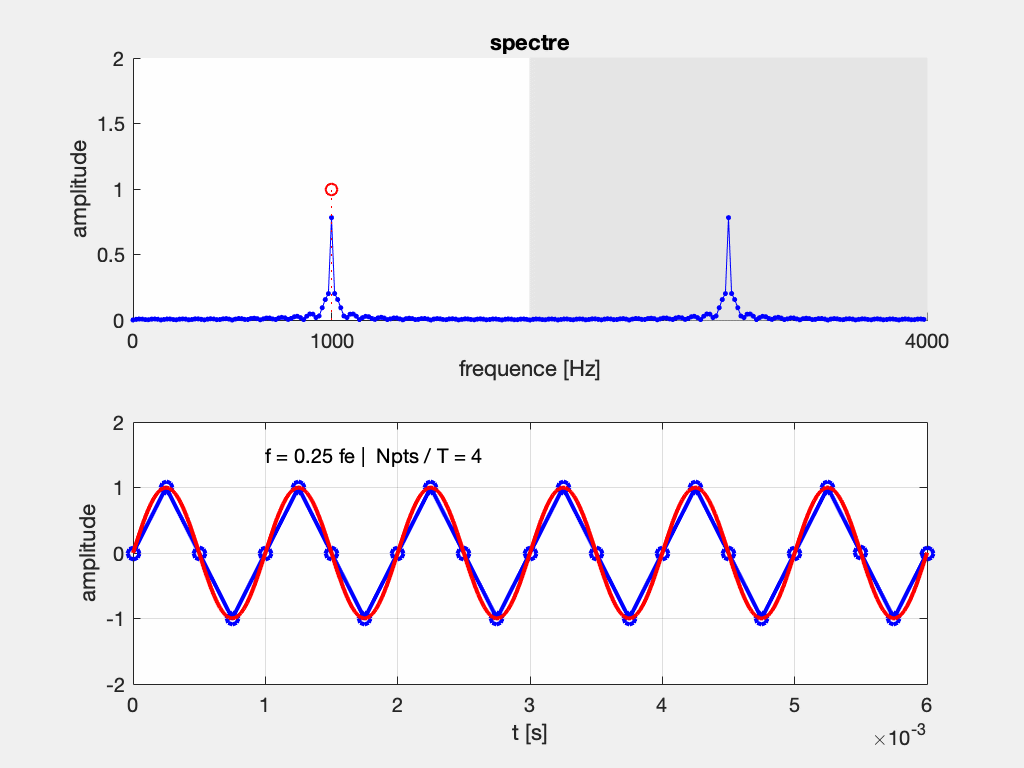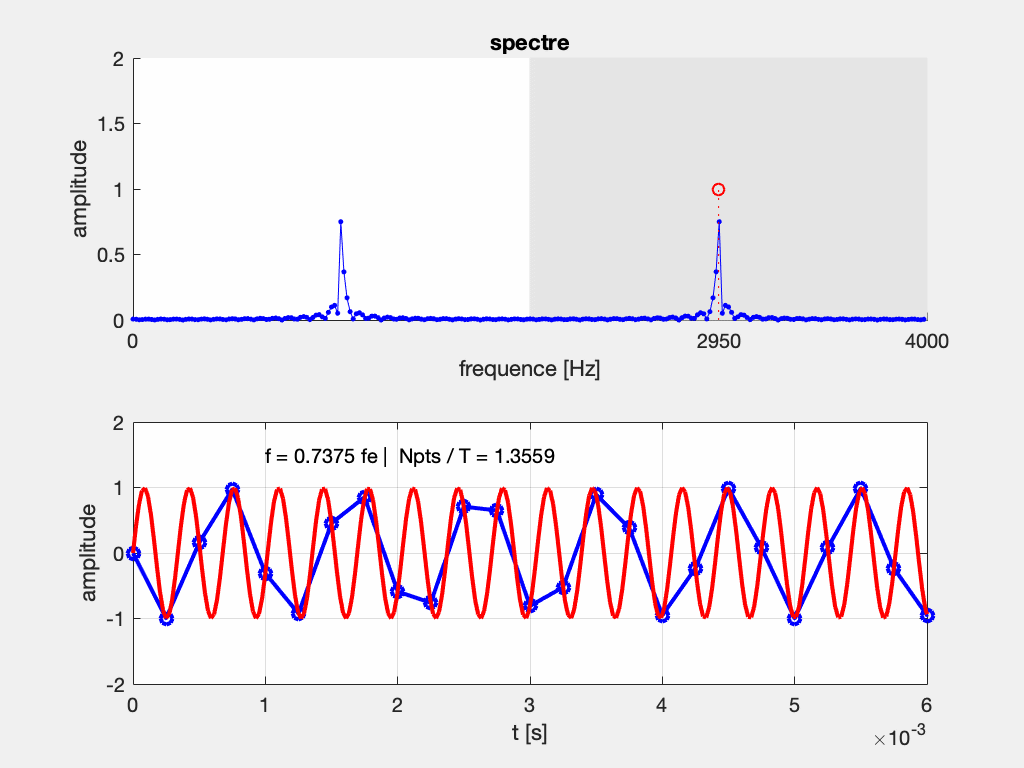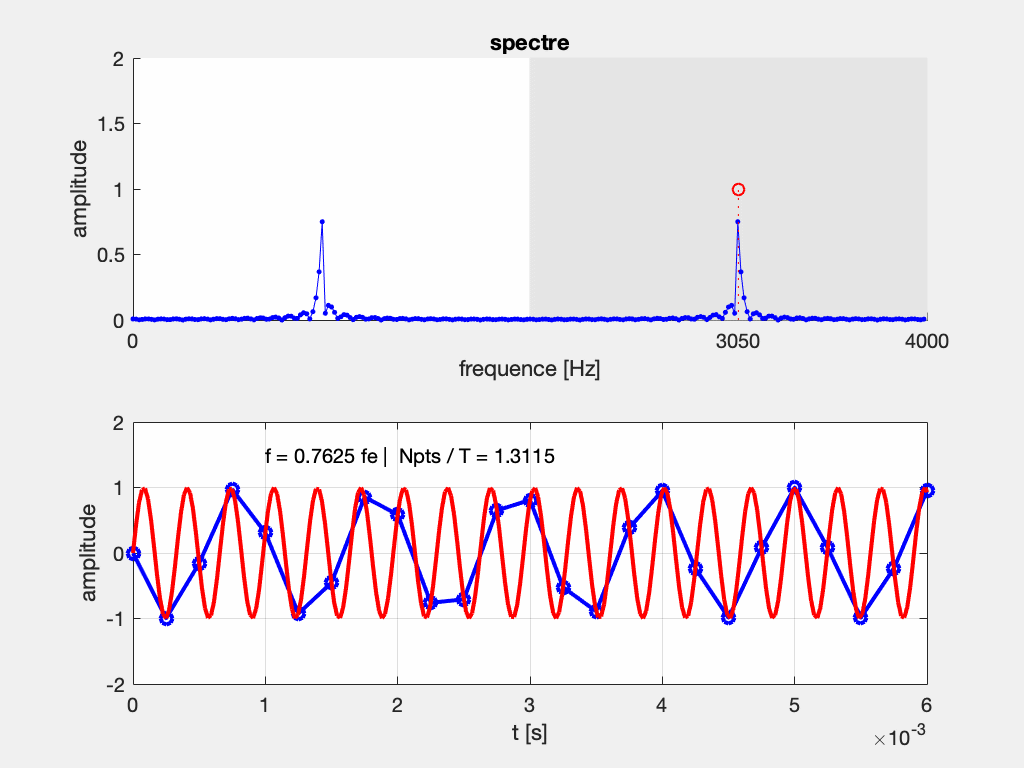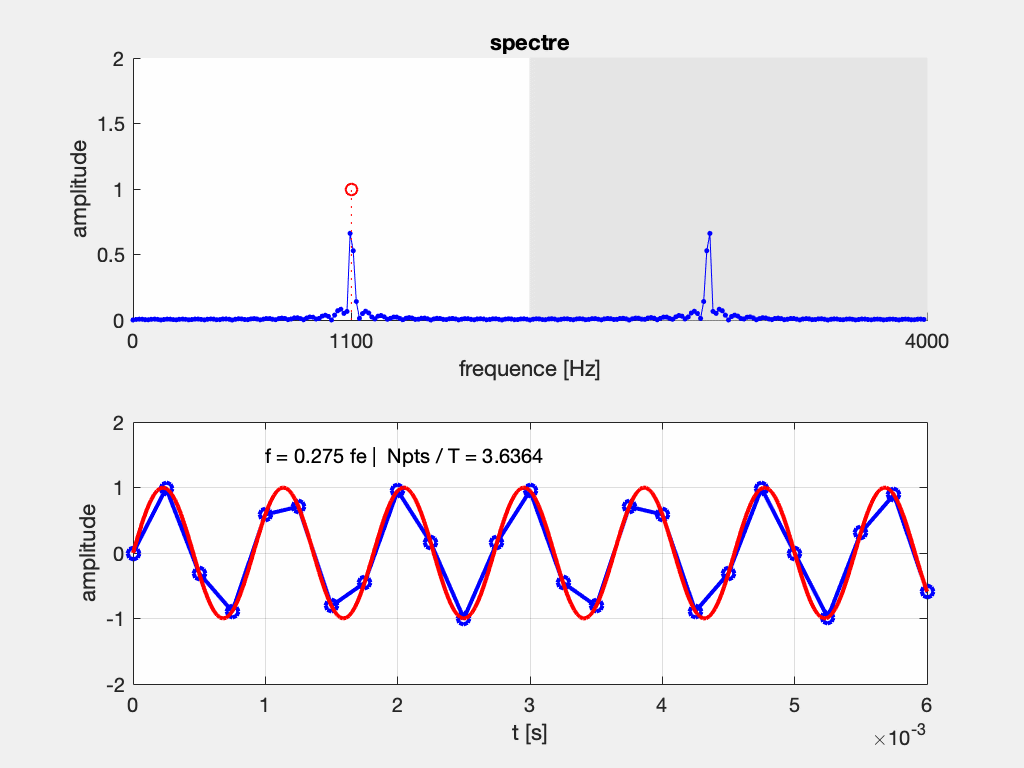
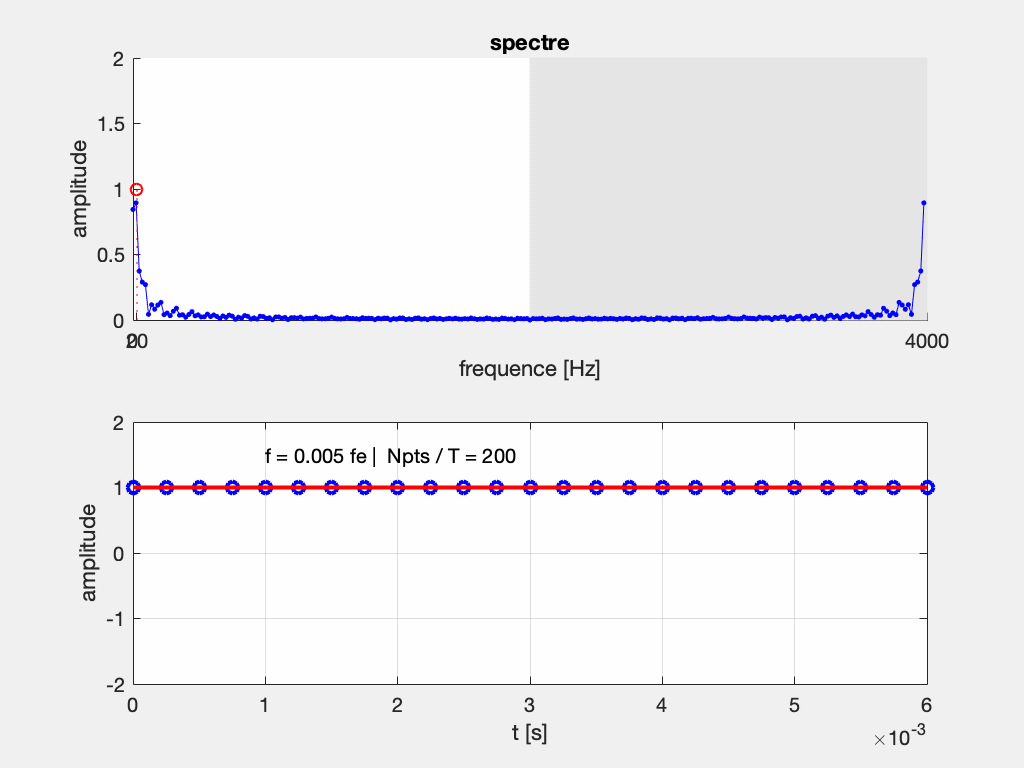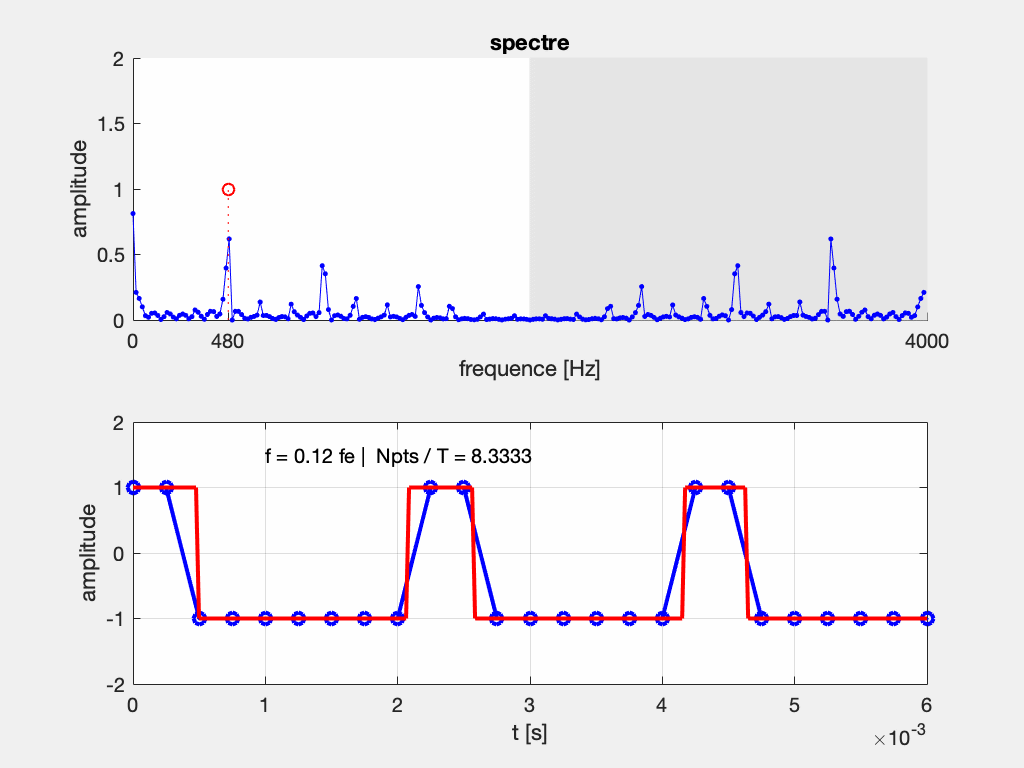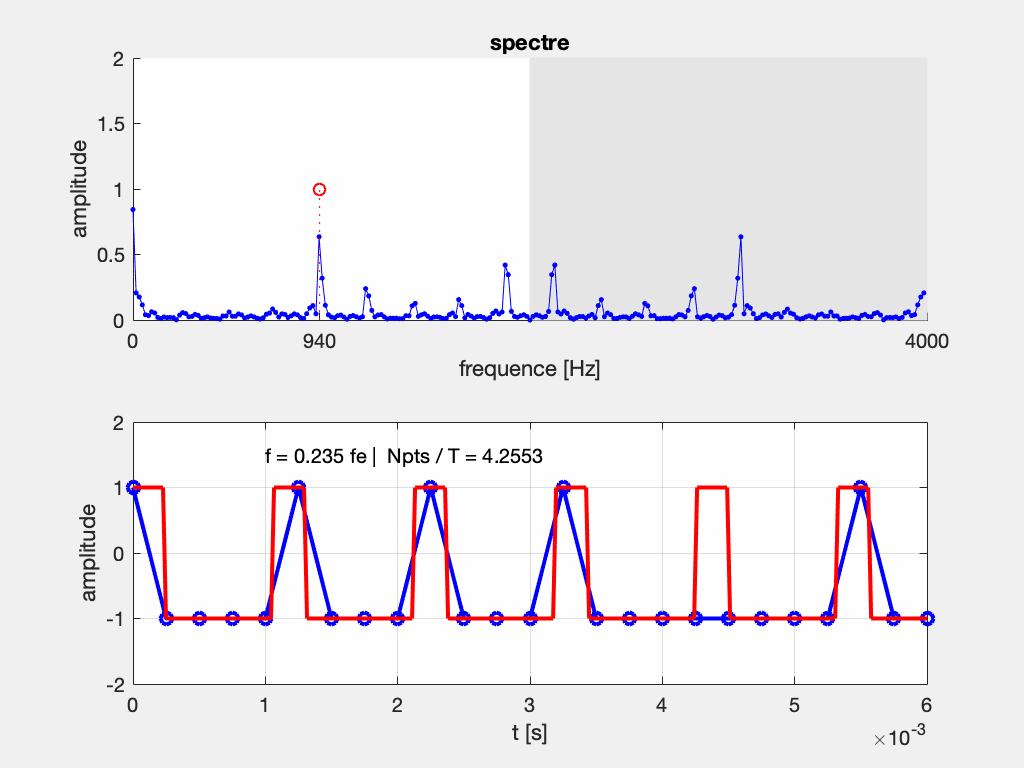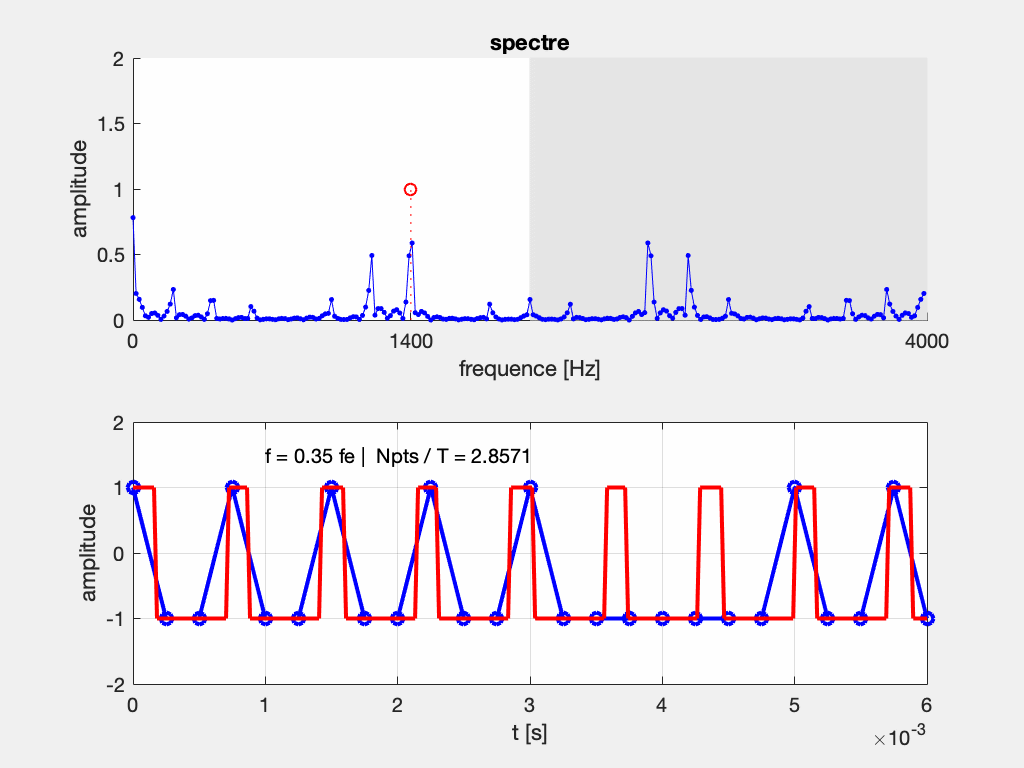
Que se passe-t-il si le théorème de Shannon n’est pas respecté, et que l’on relève moins de 2 échantillons par période ?
Si on considère l’exemple d’un échantillonnage à Fe = 2000 Hz d’un signal à F = 800 Hz, on s’apperçoit que plusieurs sinusoïdes passent par ces points. Elles sont telles que leur fréquence vaut (\pm n F_e) \pm F, c’est-à-dire : (\pm) 800 Hz, 1200 Hz, 2800 Hz, 3200 Hz, 4800 Hz, …
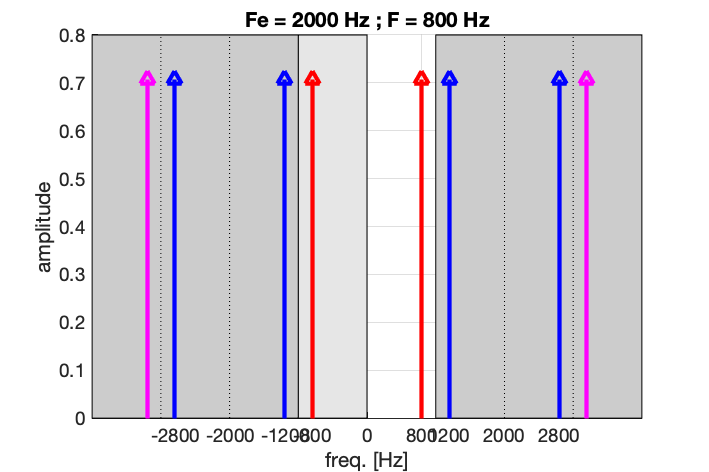
En pratique, on n’affiche sur les appareils de mesure que les composantes entre 0 et F_e/2, soit ici entre 0 et 1000 Hz.
Si maintenant on ne respecte pas le théorème de Shannon, avec un échantillonnage à Fe = 2000 Hz d’un signal à F = 1200 Hz, on s’apperçoit que plusieurs sinusoïdes passent par ces points. Elles sont telles que leur fréquence vaut (\pm n F_e) \pm F, c’est-à-dire : (\pm) 800 Hz, 1200 Hz, 2800 Hz, 3200 Hz, 4800 Hz, …
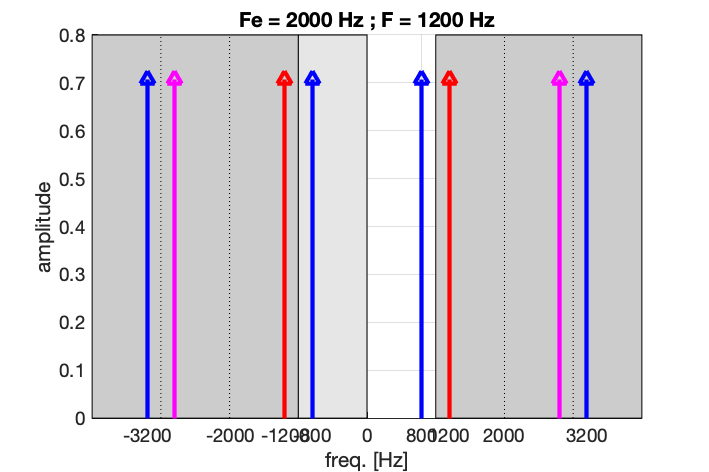
On peut interpréter le repliement du spectre comme une conséquence de sa périodisation.
Pour éviter ce phénomène, la plupart des cartes d’acquisition de qualité ont un filtre passse-bas spécifiquement conçu pour filtrer les fréquences supérieures à F_e/2 et éviter le repliement du spectre. On appelle ces filtres des Filtres anti-repliement (ou anti-aliasing)
Mais tous les appareils n’en sont pas équipés. En particulier, beaucoup d’oscilloscope numériques proposent une fonction d’analyse du spectre (FFT), mais n’ont pas de filtre anti-repliement.
Voilà ce qui peut se passer si vous analysez des fonctions à fréquence variable (balayage fréquentiel, ou frequency sweep) sur un oscilloscope numérique sans filtre anti-repliement :
La numérisation du signal implique l’analyse par transformation de Fourier discrète (TFD), et engendre également un spectre discret, connu seulement à des fréquences f_n = n \Delta f, où \Delta f est la résolution fréquentielle.
Lorsque l’on calule le spectre avec un algorithme FFT (Fast Fourier Transform), en fixant un nombre dce points N_{FFT}, la résolution fréquentielle est \Delta f = F_e/N_{FFT}. A noter: N_{FFT} peut être égal ou non au nombre d’échantillons enregistrés dans le domaine temporel. Souvent N_{FFT} est une puissance de 2 (512, 1024, 2048, ….etc).
Lorsque l’on utilise un logiciel, ou un appareil (analyseur de spectre, oscilloscope numérique, collecteur de données, …), le nombre de points que l’on règle est généralement le nombre de points qui sera affiché, et pas le nombre de points utilisés pour le calcul. Le nombre de points affiché concerne une plage de fréquence inférieure à N_{FFT}/2. Par exemple, dans le cas d’un spectre calculé sur N_{FFT}=1024 points, si un appareil affiche le spectre dans l’intervalle [0, Fe/2.56], il s’affichera sur 1024/2.56 = 400 points. Ce nombre de points affichés est parfois appelé nombre de lignes dans certains logiciels ou appareils de mesure.
Le fait de discrétiser l’axe des fréquences a pour conséquence que l’on ne peut pas détecter des évolutions du spectres sur des intervalles de fréquence très étroits. On considère en général qu’il n’est possible de bien distinguer deux pics d’amplitude que s’ils sont séparés d’au moins 8 points. Cette limite peut être une base pour déterminer le nombre de points nécessaires, ou la fréquence d’échantillonnage si le nombrre de points est fixé. Si la résolution fréquentielle est inssufisante, alors on ne sera pas capable de distinguer les différentes composantes fréquentielles.
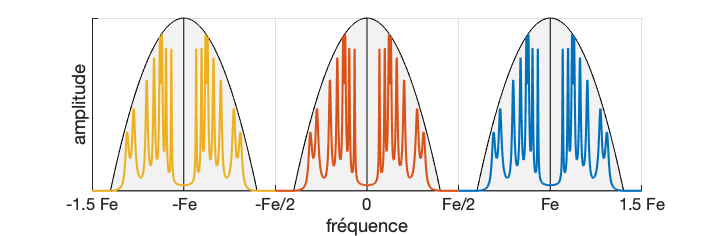
Exemples de spectres discrets obtenus par FFT



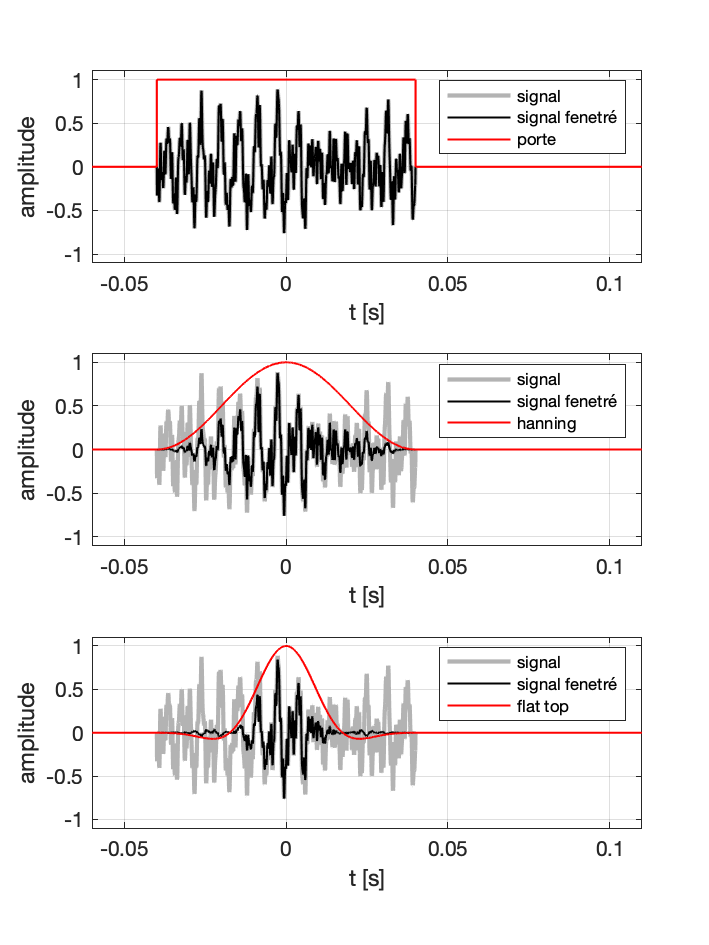
Pour limiter les artefacts dus à la troncature du signal (qui est en pratique tronqué, c’est-à-ire de dirée finie), on “adoucit” les disccontinuités au début et à la fin de l’enregistrement.
Pour cela on applique ce que l’on apppelle des fenêtres de pondération qui donnenent moins de “poids” au début et à la fin de l’enregistrement.
Les fenêtre les plus courantes sont : la fenêtre dite carrée (ou rectangle ou porte), la fenêtre de Hann (ou Hanning), la fenêtre dite flat top (dessus plat).
On utilise aussi d’autres fenêtres dans certains cas : Hamming, Tuckey, Blackman, …
Les fenêtre de pondération ont pour effet notamment de modifier la forme des pics du spectre
En général, si on ne connaît ni précisément la fréquence, ni l’amplitude des phénomènes observés, on choisit généralement une fenêtre de pondération de type Hann (appelée aussi Hanning).
Si on connaît précisément la fréquence (par exemple parce que l’on connaît la fréquence d’excitation d’un système), alors on peut préférer une fenêtre de pondération de type “Flat Top”.
…
Quel sont les critères importants ?
Capacité à détecter les fréquences
Qualité du signal
Résolution fréquentielle : détermine la capacité à distinguer les phénomènes
Taille mémoire :
si on fixe la durée d’acquisition, le signal numérique sera d’autant plus volumineux (nombre de points) que F_e est élevée
Si on fixe le nombre de points d’acquisition, alors on numérise une portion plus courte du signal (influence la qualité de l’aanalyse)
voir le paragraphe sur l’analyse fréquentielle Spectre