8 Théorème de Shannon, repliement du spectre - TRES IMPORTANT !
Le théorème de Shannon, appelé aussi Nyquist-Shannon, ou encore théorème de l’échantillonnage, énonce que l’échantillonnage d’un signal exige un nombre d’échantillons par unité de temps supérieur au double de l’écart entre les fréquences minimale et maximale qu’il contient.
En pratique, comme il est fréquent que la fréquence minimale est très inférieure à la fréquence maximale, voire qu’elle est nulle (si composante continue), on retiendra qu’il faut que la fréquence d’échantillonnage soit supérieure au double de la plus haute fréquence du signal F_{max} :
\boxed{F_e > 2 \ F_{max}}
On peut aussi dire de manière équivalente :
\boxed{F_{max} < F_e / 2 \ }
Que se passe-t-il si le théorème de Shannon n’est pas respecté, et que l’on relève moins de 2 échantillons par période ?
Si on considère l’exemple d’un échantillonnage à Fe = 2000 Hz d’un signal à F = 800 Hz, on s’apperçoit que plusieurs sinusoïdes passent par ces points. Elles sont telles que leur fréquence vaut (\pm n F_e) \pm F, c’est-à-dire : (\pm) 800 Hz, 1200 Hz, 2800 Hz, 3200 Hz, 4800 Hz, …
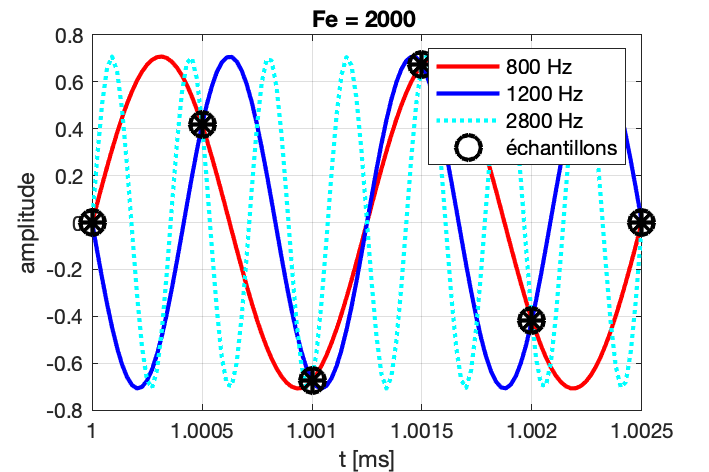
- On peut voir ce phénomène comme si le spectre était “périodisé”, tous les F_e, à quoi s’ajoute la symmétrie autour de 0, \pm F_e, \pm 2 F_e, etc.
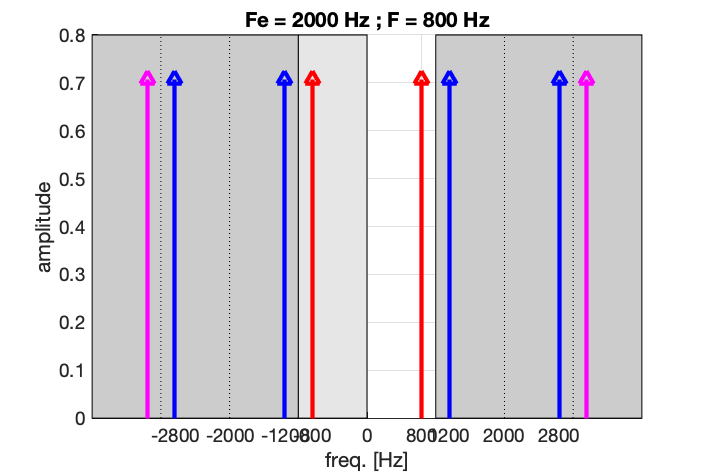
En pratique, on n’affiche sur les appareils de mesure que les composantes entre 0 et F_e/2, soit ici entre 0 et 1000 Hz.
Si maintenant on ne respecte pas le théorème de Shannon, avec un échantillonnage à Fe = 2000 Hz d’un signal à F = 1200 Hz, on s’apperçoit que plusieurs sinusoïdes passent par ces points. Elles sont telles que leur fréquence vaut (\pm n F_e) \pm F, c’est-à-dire : (\pm) 800 Hz, 1200 Hz, 2800 Hz, 3200 Hz, 4800 Hz, …
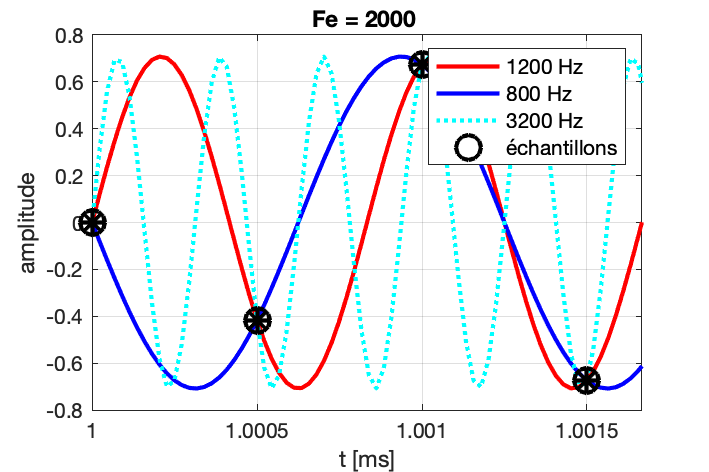
- Et comme le signal que l’on peut reconstruire à partir des points échantillonnés sera cette fois la sinusoïde à 800 Hz, … on ne va pas analyser la bonne fréquence !
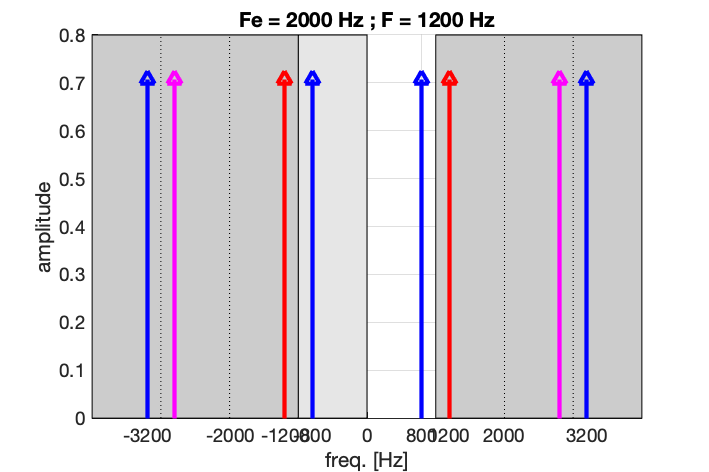
On parle alors alors de repliement du spectre. En anglais, cet “effet mirroir” est appelé aliasing.
On peut interpréter le repliement du spectre comme une conséquence de sa périodisation.
Pour éviter ce phénomène, la plupart des cartes d’acquisition de qualité ont un filtre passse-bas spécifiquement conçu pour filtrer les fréquences supérieures à F_e/2 et éviter le repliement du spectre. On appelle ces filtres des Filtres anti-repliement (ou anti-aliasing)
Mais tous les appareils n’en sont pas équipés. En particulier, beaucoup d’oscilloscopesr numériques proposent une fonction d’analyse du spectre (FFT), mais n’ont pas de filtre anti-repliement.
Voilà ce qui peut se passer si vous analysez des fonctions à fréquence variable (balayage fréquentiel, ou frequency sweep) sur un oscilloscope numérique sans filtre anti-repliement :
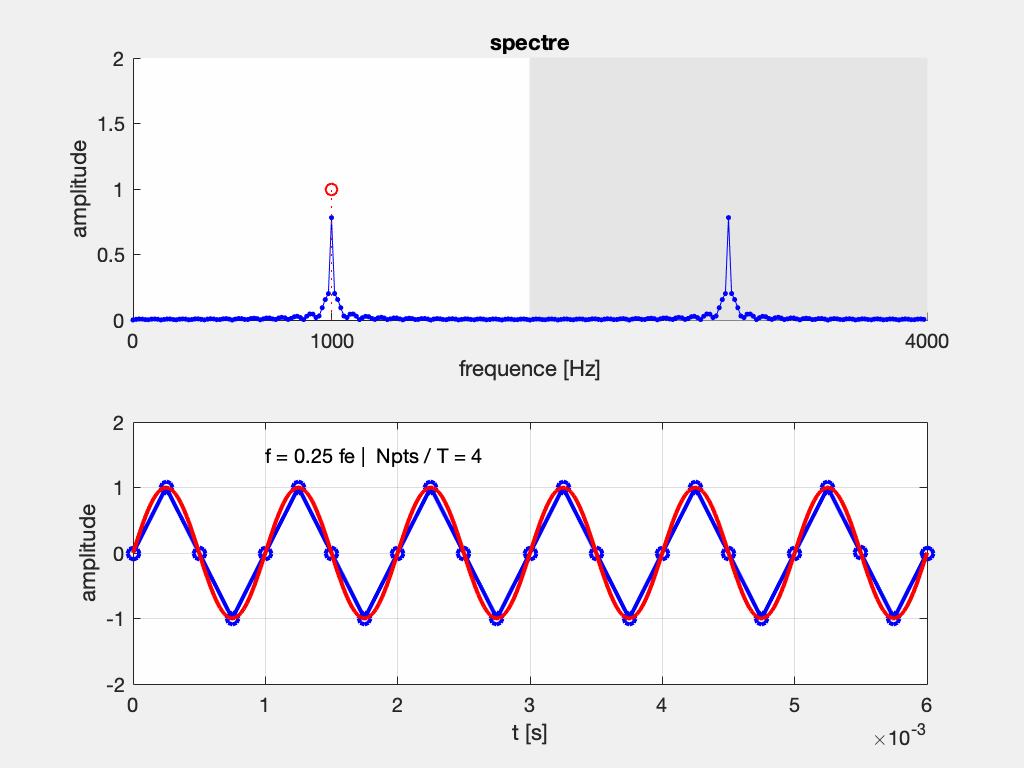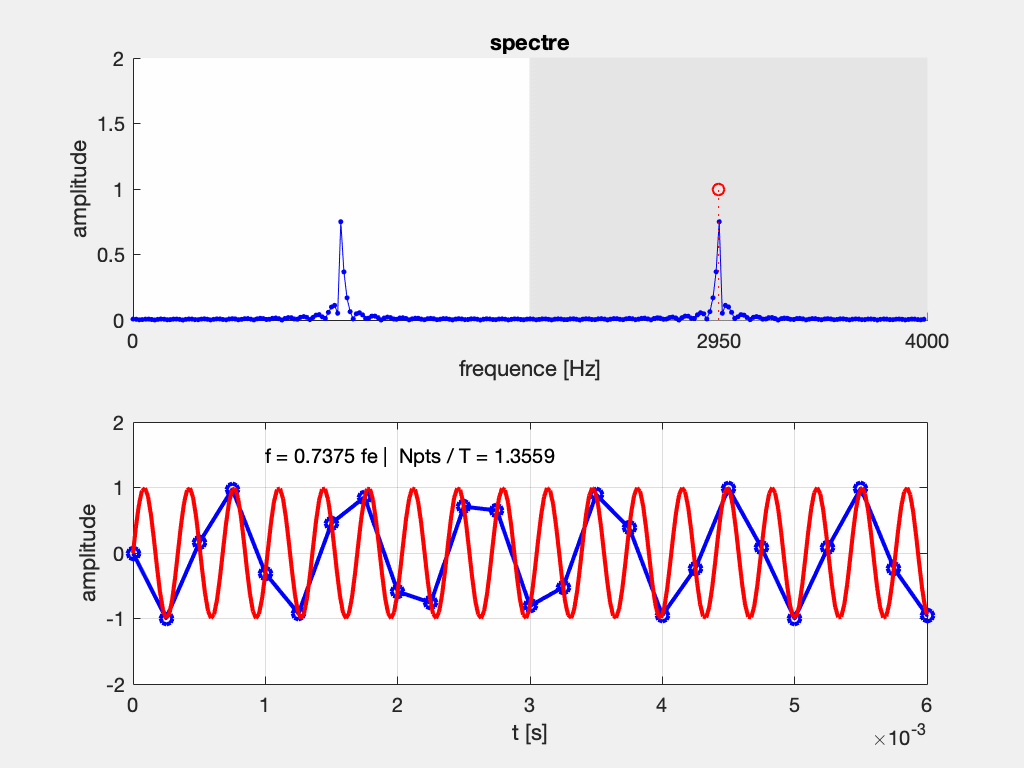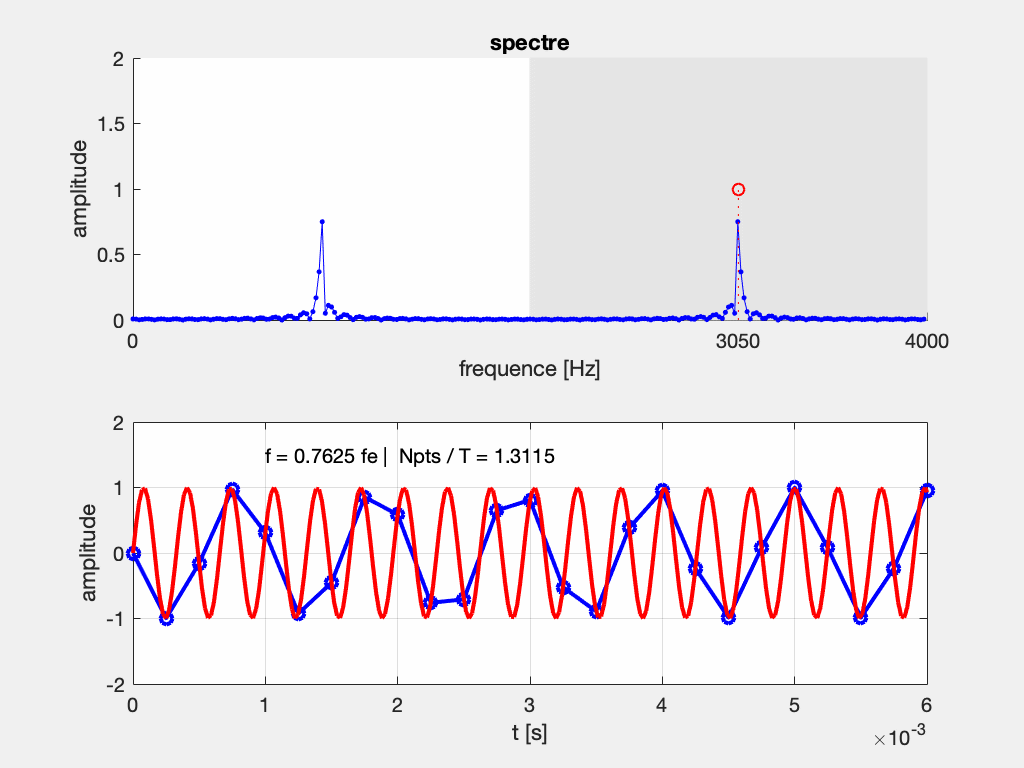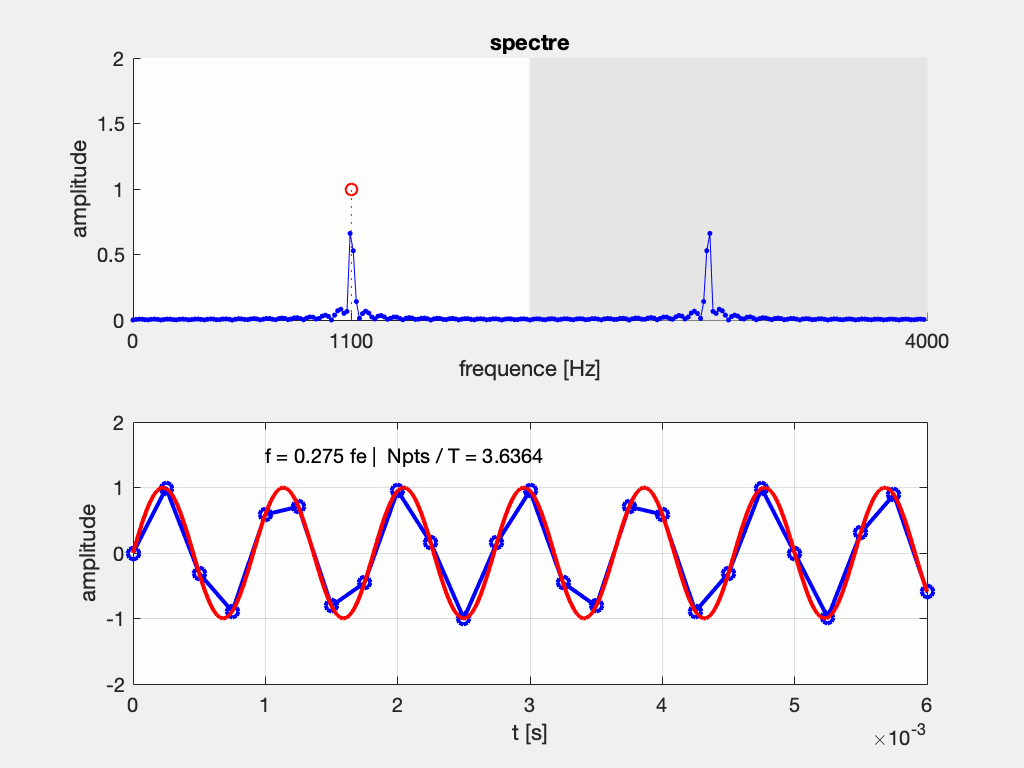
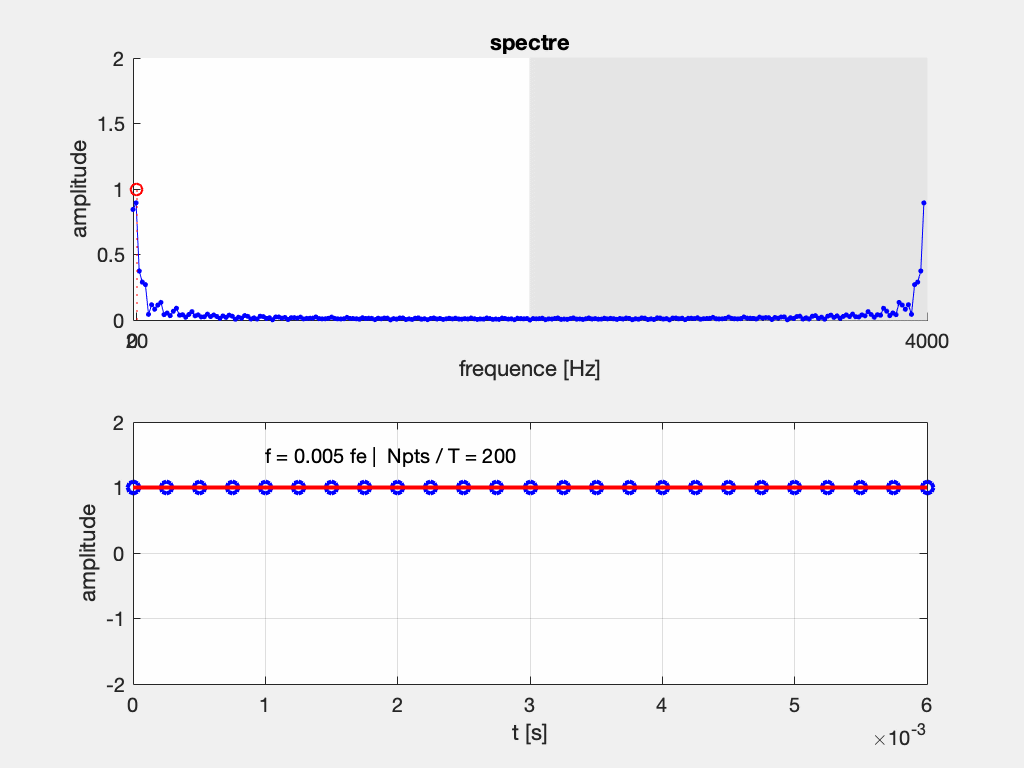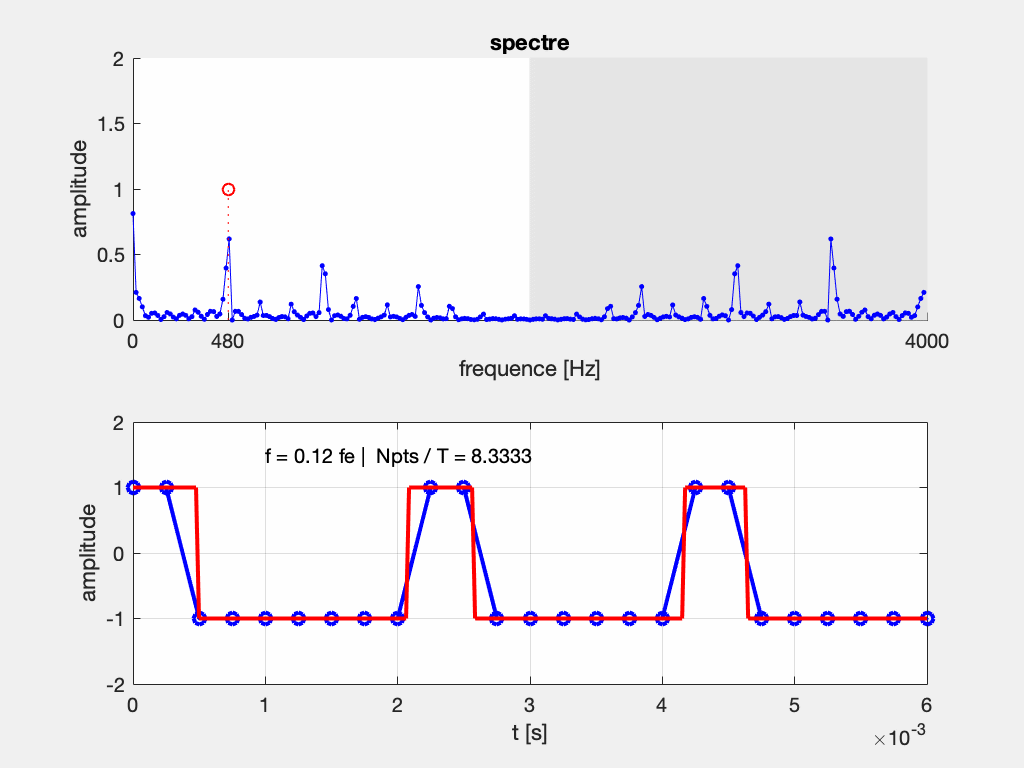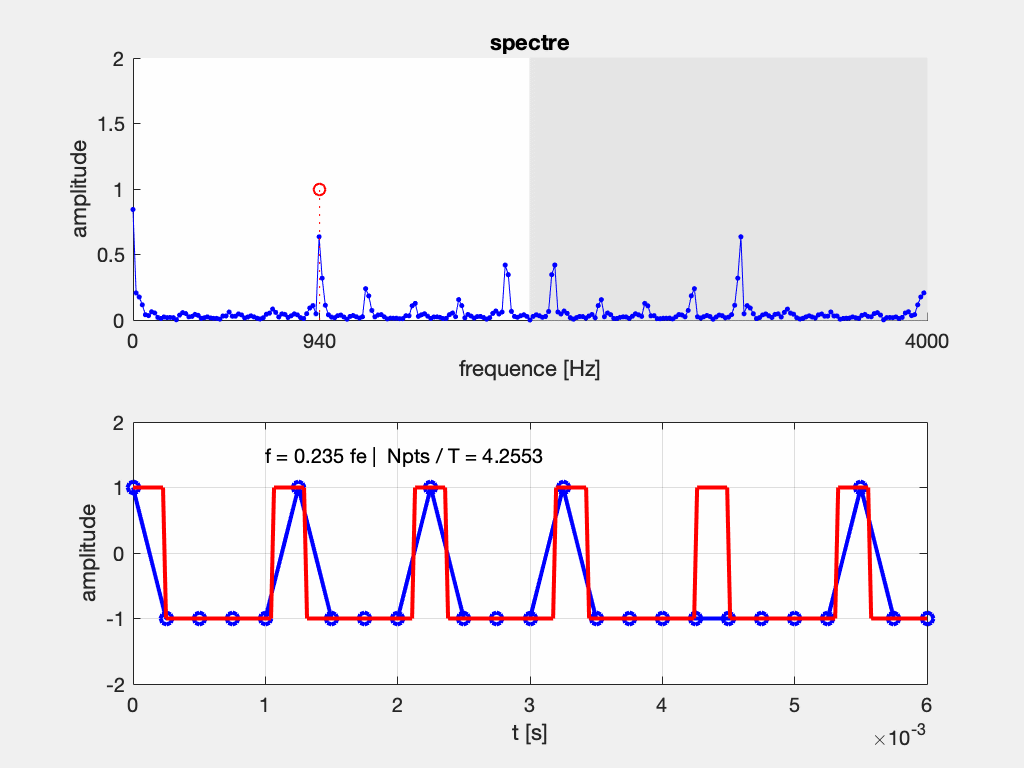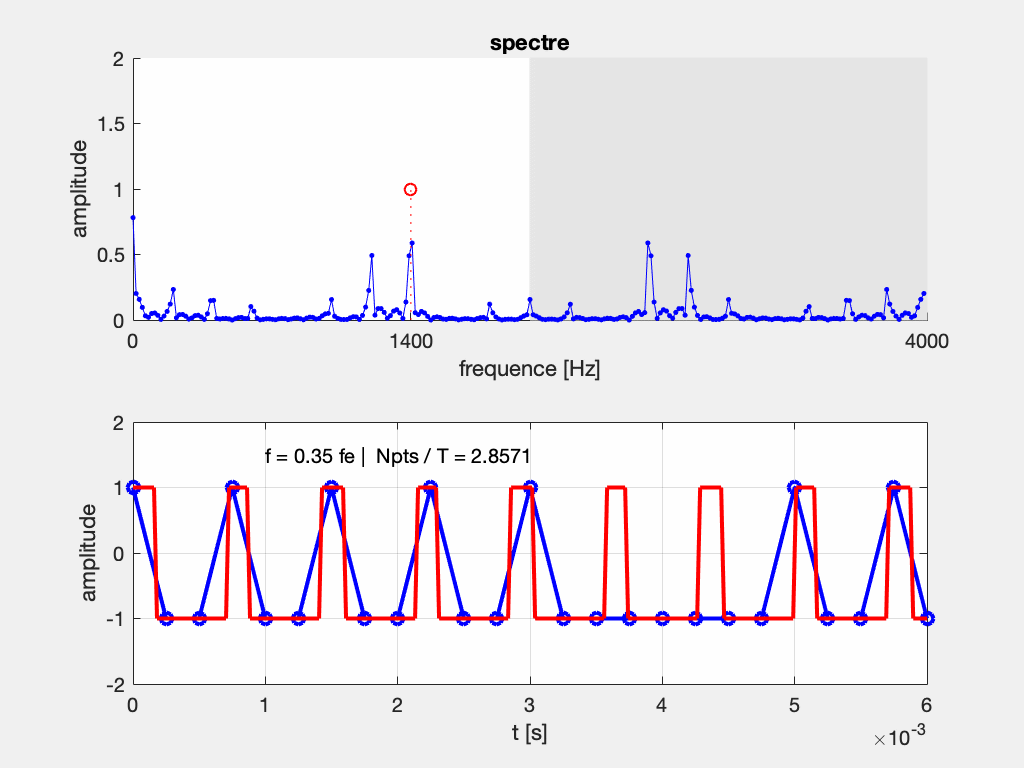
Commentaires :
Image du bas : Le signal original (en rouge) est la sinusoïde de fréquence F variable (“sweep sine” sur un GBF). Le signal bleu est le signal échantillonné à une fréquence fixe F_e. On observe que si la période diminue (c-à-d si la fréquence augmente), la fréquence d’échantillonnage n’est pas suffisante pour relever plus de 2 échantillons par période, et la fréquence du signal bleu parait plus basse que le signal original.
image du haut : On représente le résultat de l’analyse fréquentielle du signal numérisé (en bleu) et la position du pic correspondant au signal original (cercle rouge). On remarque que lorsque F > F_e /2, le pic à F sort de la fenêtre d’observation (intervalle [0,F_e/2]) tandis que son symétrique de fréquence F_e-F rentre dans la fenêtre d’observation. C’est cette fréquence plus basse que F que l’on a observé sur le signal temporel. On a l’impression d’un “repliement” du spectre, ou encore d’un effet mirroir.
NB: Ce phénomène est observabe en TP avec un GBF et un oscilloscope numérique (qui n’ont le plus souvent pas de filtre pour éviter ce phénomène)
Dans le cas de signaux plus complexes, l’interprétation du spectre est parfois subtile losqu’il y a repliement. Par exemple ci-dessous dans le cas d’un signal rectangle de fréquence glissante et à rapport cyclique constant. On observe que même si la fréquence fondamentale du signal respecte le critère de Shannon, ses harmoniques peuvent avoir une fréquence supérieure à F_e/2. On observe une partie des harmoniques qui se déplacent de droite à gauche lorsque la fréquence augmente, mais les harmoniques issus du repliement du spectre se déplacent de droite à gauche car leur fréquence est > F_e/2.
NB: Ce phénomène est observabe en TP avec un GBF et un oscilloscope numérique (qui n’ont le plus souvent pas de filtre pour éviter ce phénomène)