5 Signaux périodiques : séries de Fourier
L’analyse des fréquences des signaux périodiques est vue en cours de mathématiques dans le cours sur les séries de Fourier.
l’analyse spectrale est appelée analyse de Fourier en référence au Mathématicien et Physicien Joseph Fourier [wikipedia]
Sans développer un cours de mathématiques ici, on présente ci-dessous quelques éléments sur la décomposition en séries de Fourier (voir le cours de Mathémaiques pour plus de détails)
A RETENIR : Les signaux périodiques sont constitués de composantes dites harmoniques, c’est-à-dire telles que les fréquences F_{nh} des différentes composantes du signal ont des fréquences liées à une fréquence fondamentale F_0 de la manière suivante :
F_{nh} = n F_0, \ \ \text{avec} \ \ n= 1, 2, 3, 4, ...
Remarque : toutes les composantes n ne sont pas forcément présentes dans le signal, ou, autrement dit, certaines peuvent avoir une amplitude A_n nulle. La fondamentale peut également avoir une amplitude nulle.
- Exemple :
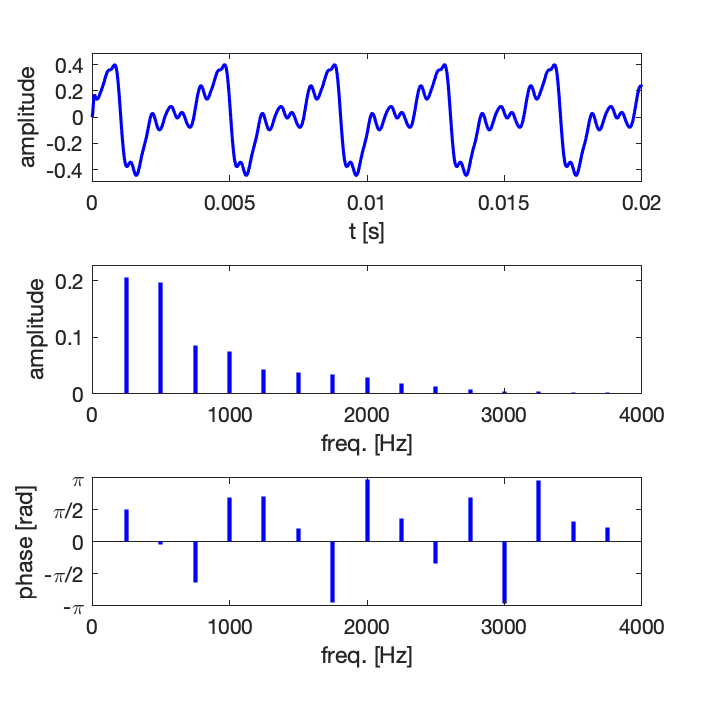
exemple_signal_periodique_serie_Fourier.mp3
5.1 Décomposition en fonctions sinus et cosinus :
Avertissements :
Il ne s’agit pas ici d’être complet, mais de présenter quelques notions de base avant de consulter un cours dédié aux séries de Fourier. On se place dans un contexte d’analyse de signaux réels, issus par exemple de capteurs et d’appareils de mesure.
On aborde souvent la décomposition de signaux périodiques s(t) sous la forme de séries du type
S_n (t) = a_0 + \sum_{n=0}^{n=N} a_n \sin(n \omega_0 t) + \sum_{n=0}^{n=N} b_n \sin(n \omega_0 t) où :
n = 1, 2, 3..., a_0, a_n, et b_n sont des coefficients réels;
\omega_0, f_0 = \omega_0 / (2 \pi), et T_0 = 2 \pi / \omega sont la pulsation, la fréquence, et la période fondamentales.
On peut écrire la série en faisant apparaître l’argument des fonctions sinus ou cosinus sous différentes formes : (n \omega_0 t) ou ( 2 \pi n f_0 t), ou encore (n 2 \pi t / T_0 ).
On trouve aussi des formes où l’on fait apparaître \omega_n = n \omega_0, f_n = n f_0.
Les coefficients a_0, a_n, et b_n se déterminent comme ceci :
le coefficient a_0 correspond à la composante continue du signal (sa moyenne sur une période) :
a_0 = \frac{1}{T_0} \int_0^{T_0} s(t) \rm{d}t
Les autres coefficients peuvent être vus comme une projection sur une base de fonctions, de manière similaire à la décomposition de vecteurs en composantes selon des vecteurs de base.
coefficients a_n, avec n\geq 1, et f_n = n \ f_0 :
a_n = \frac{1}{T_0} \int_0^{T_0} s(t) \sin(2 \pi f_n \ t)\rm{d}t
coefficients b_n, avec n\geq 1, et f_n = n \ f_0 :
b_n = \frac{1}{T_0} \int_0^{T_0} s(t) \cos(2 \pi f_n \ t)\rm{d}t
Remarque importante : Le nombre N de composantes harmoniques à prendre en compte dépend du signal. Ce nombre peut être fini, ou infini. Lorsque le nombre de composantes n’est pas suffisant, le signal S_n(t) diffère du signal original s(t).
Exemple 1 : synthèse d’un signal de forme dent de scie avec un nombre croissant de composantes harmoniques : 5, 10, 15
Comme en pratique la série ne peut pas être infinie, on observe des oscillations résiduelles, il s’agit du phénomène de Gibbs [en savoir plus sur Wikipedia].
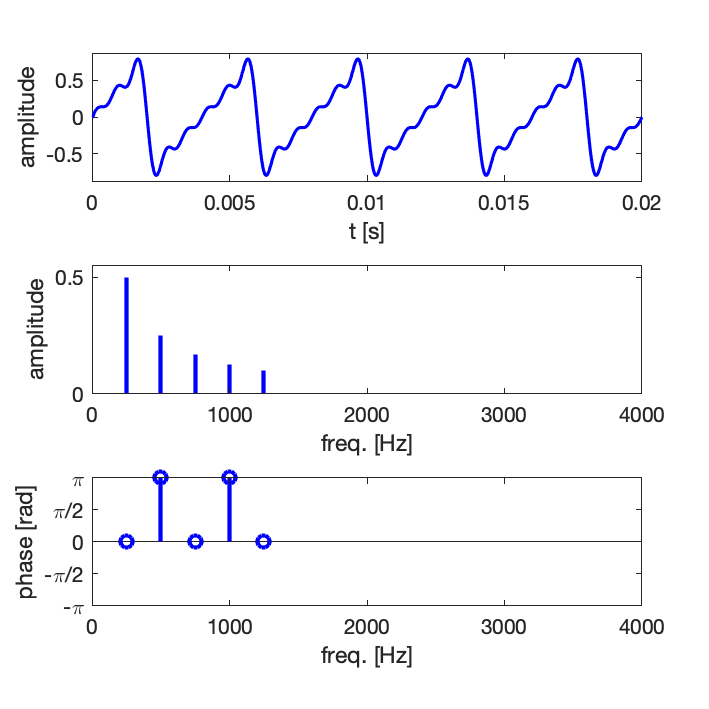
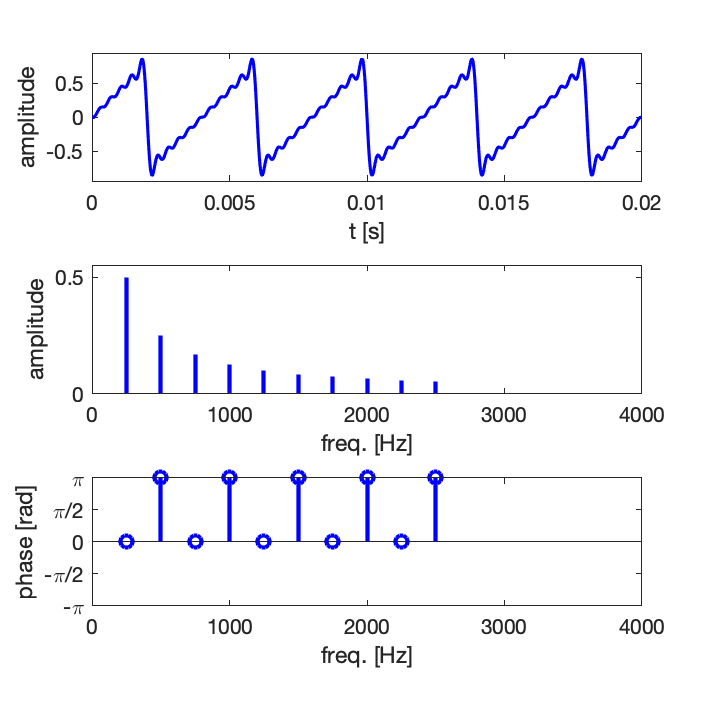
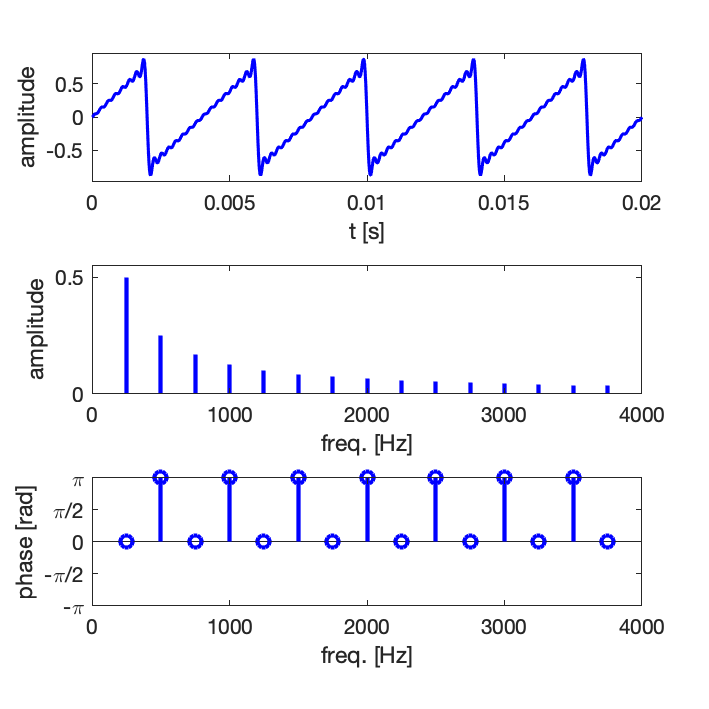
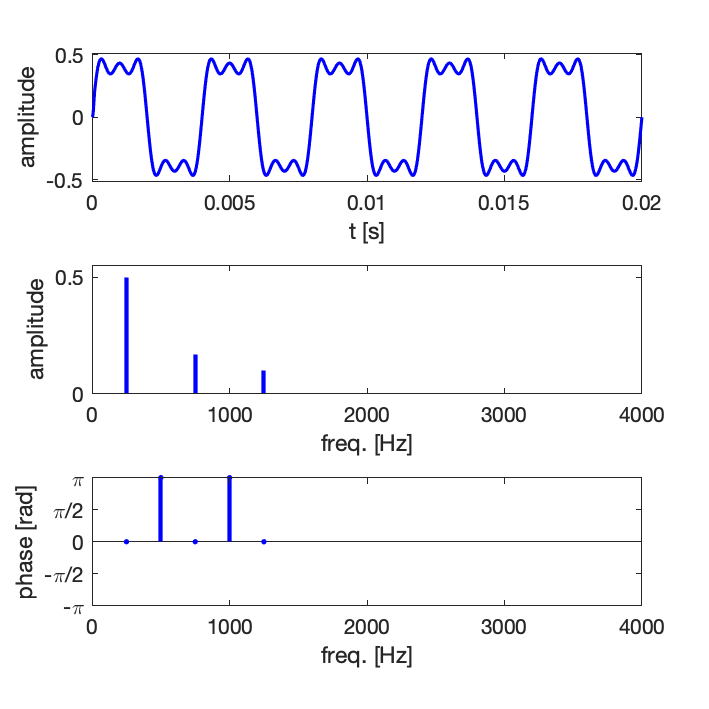
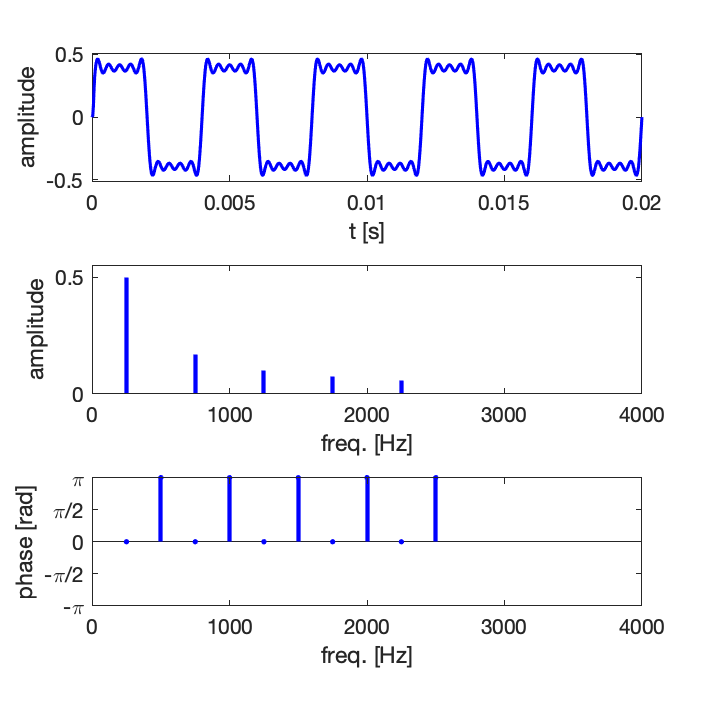
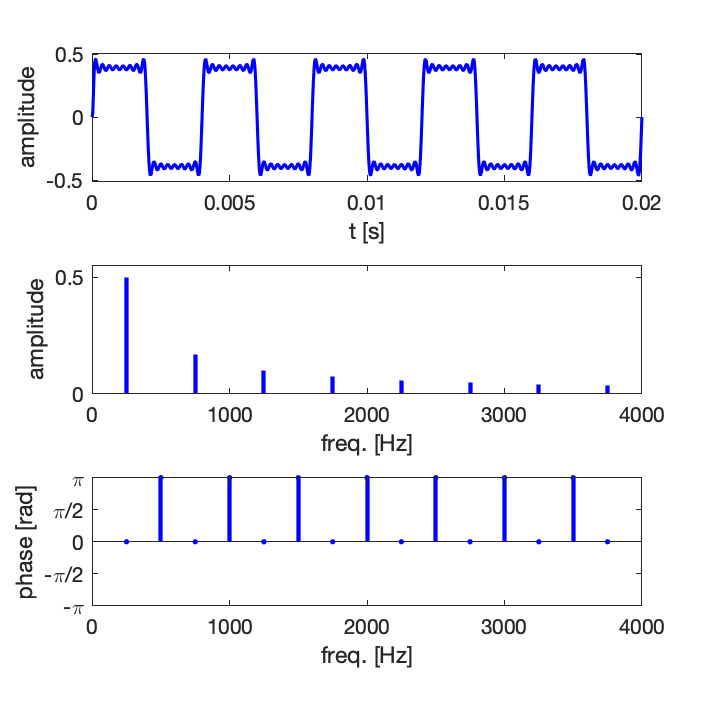
Exemple 2 : synthèse d’un signal de type carré avec un nombre croissant de composantes harmoniques : 5, 10, 15
Comme en pratique la série ne peut pas être infinie, on observe des oscillations résiduelles, il s’agit du phénomène de Gibbs [en savoir plus sur Wikipedia].
5.2 Décomposition en fonctions sinus ou cosinus
On peut aussi écrire la décomposition en série de Fourier de la manière suivante :
S_n (t) = a_0 + \sum_{n=0}^{n=N} A_n \sin(2 \pi f_n \ t + \phi_n)
ou encore
S_n (t) = a_0 + \sum_{n=0}^{n=N} A_n \cos(2 \pi f_n \ t + \psi_n)
avec f_n = n \ f_0
5.3 Décomposition en fonctions exponentielles complexes
Les fonctions sinus et cosinus pouvant être décomposées en exponentielles, on peut aussi écrire les séries de Fourier en utilisant les fonctions exponentielles complexes :
\displaystyle S_n = \sum _{n=-\infty }^{+\infty }c_{n}{\rm {e}}^{{\rm {j}}2 \pi f_n \ t}
avec f_n = n \ f_0 (remarque : pour n=0, on retrouve a_0)
Remarque : en électricité et en physique, pour éviter la confusion avec le symbole du courant électrique, on préfère souvent nommer le nombre complexe \sqrt{-1} en utilisant la lettre j au lieu de la lettre i, qui est préférée en mathématiques.
En savoir plus sur wikipedia
(NB: les notations et l’ordre des explication, plus complètes et plus rigoureuses, peuvent parfois différer des choix faits ici, où l’on se contente d’une première appproche, et avec un point de vue “pratique”, notamment en privilégiant le cas des signaux réel.)
NB : CES NOTIONS SONT OU SERONT ETUDIÉES EN DÉTAIL DANS LES COURS DE MATHÉMATIQUES