4 Représentation du spectre d’un signal simple
Considérons un signal constitué de la somme de 2 composantes sinusoïdales
- composante 1 : s_1(t) = A_1 \sin (2 \pi F_1 t + \phi_1)
- composante 2: s_2(t) = A_2 \sin (2 \pi F_2 t + \phi_2)
- Somme (ou “Mix” en audio) : s(t) = s_1 (t) + s_2 (t) =A_1 \sin (2 \pi F_1 t + \phi_1) + A_2 \sin (2 \pi F_2 t + \phi_2)
où A_1 et A_2 sont les ampltudes, F_1 et F_2 les fréquences, et \phi_1 et \phi_2 les phases par rapport à une référence commune.
- composante 1 : s_1(t) = A_1 \sin (2 \pi F_1 t + \phi_1)
Le signal et ses composantes sont représentées ci-dessous en fonction du temps, ainsi qu’en fonction de la fréquence en traçant l’amplitude et la phase des composantes :
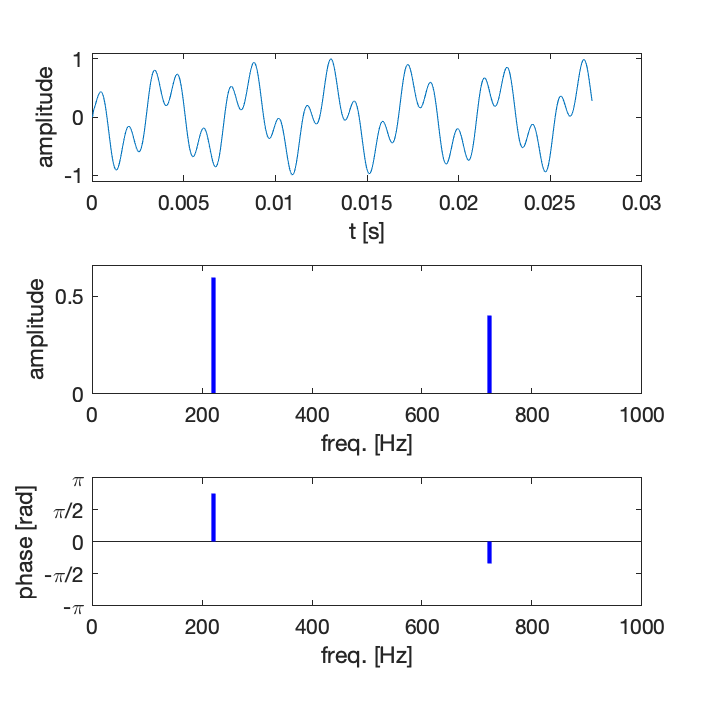
Remarques :
La phase est parfois un paramètre très important, et parfois non.
Très souvent on représente uniquement l’amplitude en échelle logarithmique par rapport à une référence, sans préciser la phase.
En pratique, on représente souvent en amplitude la valeur efficace, ou bien la puissance, ou la densité spectrale de puissance, et très souvent en échelle logarithmique.
Analyse / Synthese
pour représenter le spectre d’un signal, il faut d’abord savoir l’analyser et extraire les paramètres de chaque composante fréquentielle.
L’analyse fréquentielle vise à évaluer les amplitudes et éventuellement la phase des différentes composantes fréquentielles
On parle de synthèse lorsque l’on reconstitue le signal en sommant les différentes composantes. (En musique, la synthèse sonore par addition de composantes sinusoïdales est appelée “synthèse additive”)