3 Introduction à l’analyse fréquentielle
Dans ce qui suit on s’intéresse plus en détail à l’influence des paramètres d’échantillonnage sur l’analyse des fréquences.
Avertissement :
On se limite à introduire les notions élémentaires pour une prermière approche, en lien avec l’acquisition numérique du signal. L’ambition n’est pas d’être complet ni exhaustif. Se référer aux cours de mathématiques et consultter des ouvrages ou sites web sur le traitement du signal pour plus de précisions.
ATTENTION AU VOLUME SONORE DE VOTRE APPAREIL :
COMMENEZ PAR ÉCOUTER LES EXEMPLES SONORES À FAIBLE VOLUME
EN PARTICULIER SI VOUS UTILISEZ DES ÉCOUTEURS !!!
3.1 Du signal temporel au spectre dans un cas simple
L’ analyse fréquentielle, ou analyse spectrale consiste à analyser le contenu fréquentiel d’un signal.
Pour sensibiliser les principes et l’intérêt de l’analyse des fréquences qui constituent les signaux alternatifs, considérons d’abord le cas du signal ci-dessous, représenté en fonction du temps comme on pourrait le visualiser sur un oscilloscope :
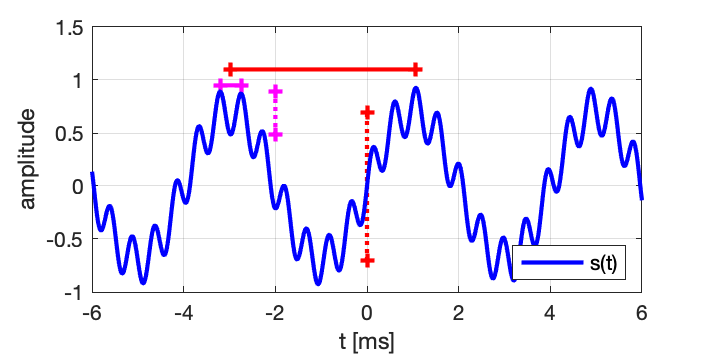
On observe bien 2 sinusoïdes superposées, et l’écoute du signal nous permet également de distinguer deux fréquences bien distinctes
signal audio :
- On distingue deux composantes :
Remarque :
Comme nous percevons mieux les fréquences élevées que les fréquences graves, malgré la différence d’amplitude que l’on peut observer, le signal de fréquence élevée nous appparaît, à l’écoute, à peu près du même niveau que la basse fréquence.
Cette sensation dépend aussi du système d’écoute (haut-parleurs, casque) et de l’appareil (ordinateur ou tablette, smartphone).
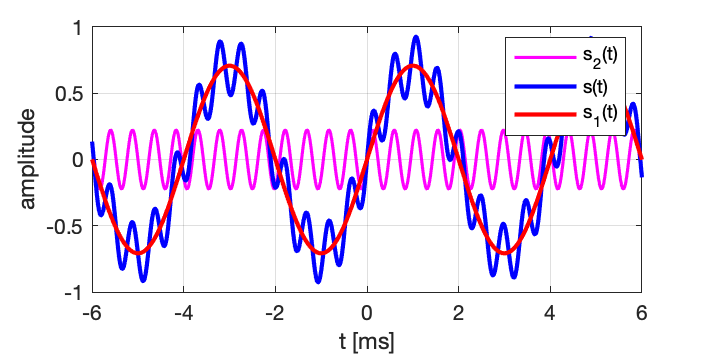
- En écoutant le signal et en observant la forme d’onde, c’est à-dire l’amplitude en fonction du temps, nous avons pu dans ce cas simple distinguer deux composantes fréquentielles, et pouvons réduire l’information pour décrire le signal temporel en précisant la fréquence et l’amplitude de ces deux composantes.
- Dans ce cas simple, l’analyse du signal temporel avec des curseurs comme sur un oscilloscope permet d’évaluer approximativement l’amplitude et la période des deux composantes, et en déduire la fréquence :
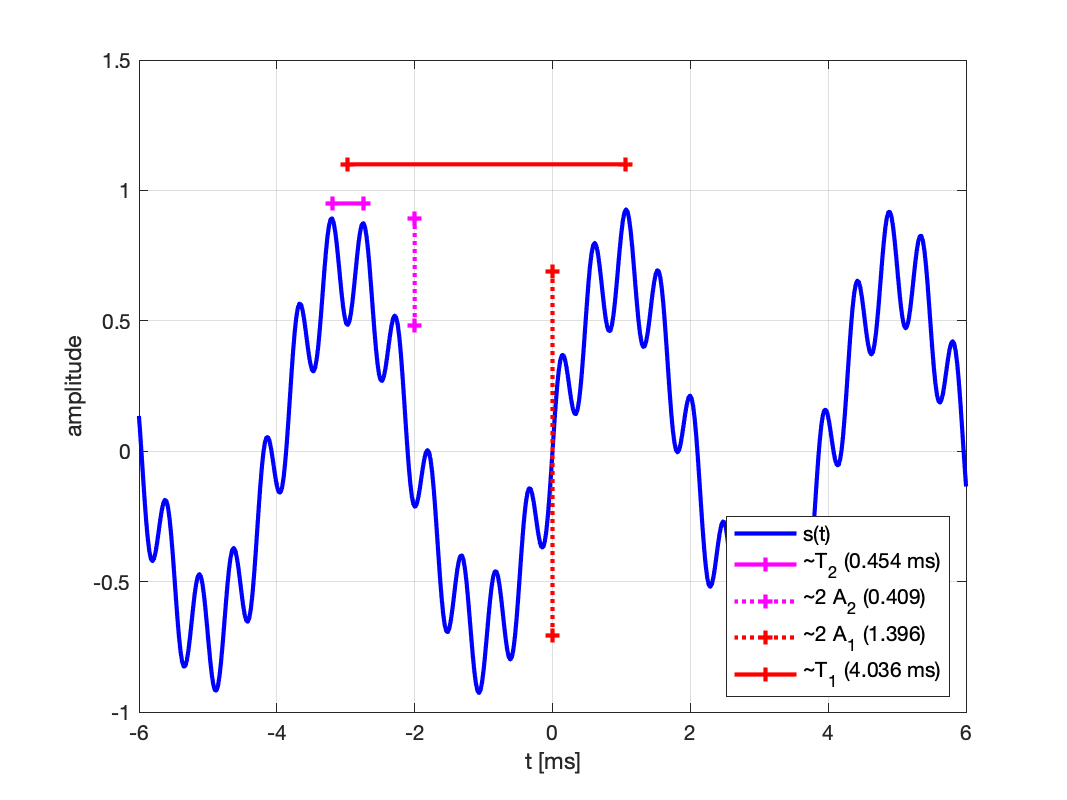
On en déduit des valeurs approchées des amplitudes et des fréquences :
\tilde{F_1}=248 Hz (valeur exacte F_1 = 250 Hz) ; \tilde{F_2}=2205 Hz (valeur exacte F_2 = 2100 Hz) ; \tilde{A_1}=0.698 (valeur exacte A_1 = 0.708) ; \tilde{A_2}=0.205 (valeur exacte A_2 = 0.224 ).
On peut alors réduire l’information et représenter le signal sous la forme d’une courbe représentant l’amplitude en fonction de la fréquence :
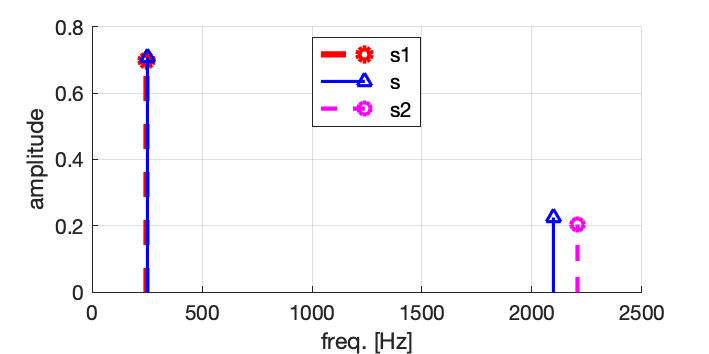
Ce type de représentation, l’amplitude en fonction de la fréquence, est le spectre du signal.
Dans de nombreuses applications, et notamment en acoustique, vibrations, audio, électronique, etc, on représente souvent les amplitudes en échelle logarithmique, et notamment en décibels.
Si on choisit arbitrairement la valeur 1 comme référence, on peut représenter l’amplitude A du signal en \rm{dB}_{ref \ 1} en calculant la valeur en décibels 20 \log\left( A / 1 \right) :
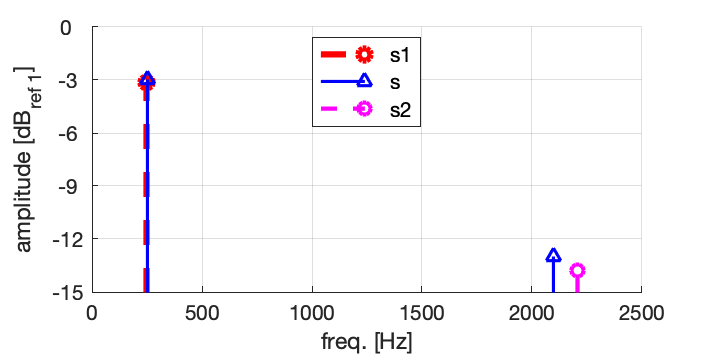
Remarque : En pratique, on utilisera des valeurs de références standard pour les dB selon la nature du signal. Par exemple: 1 Volt ou 1 \muV efficace, 1 Watt, 20 microPascals, 1 g, 1 \rm{m}/\rm{s}^2, etc.
L’exemple simple que nous venons de discuter en détails permet de comprendre que l’on peut analyser et représenter un signal en fonction de la fréquence (représentation spectrale, ou simplement spectre) au lieu d’une représentation temporelle (ou forme d’onde).
Mais pour des signaux plus complexes l’analyse ne peut pas se faire aussi simplement et il faut utiliser des outils spécifiques.
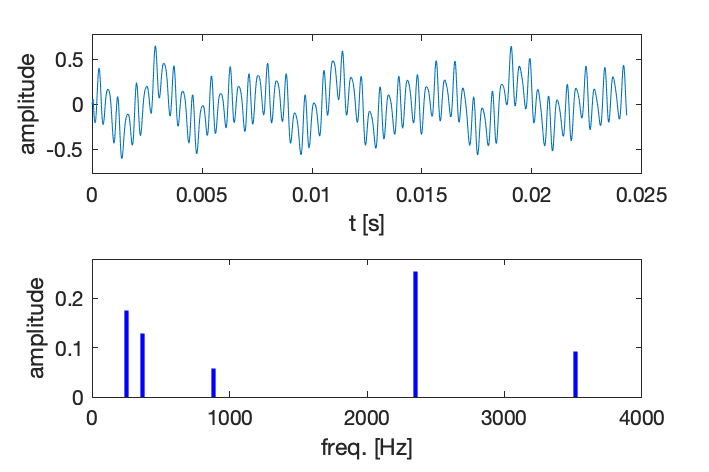
Par exemple, en écoutant le signal ci-dessous, qui contient 5 fréquences superposées, l’analyse est difficile, voire impossible, à partir du signal temporel, ou même à l’écoute. Il faut un outil d’analyse des fréquence.