2 Paramètres d’échantillonnage
On se concentre dans la suite, sur les domaines temporels et fréquentiels.
Le premier paramètre à considérer est la fréquence d’échantillonnage, qui définit le pas temporel entre deux échantillons de valeur prélevés sur le signal.
Fréquence d’échantillonnage : La fréquence à laquelle les valeurs du signal sont mémorisées.
Remarque : Cette fréquence est souvent notée F_e pour fréquence d’échantillonnage, ou souvent en anglais F_s pour sampling frequency, ou encore sr pour sampling rate. On utilisera F_e ou F_s dans la suite.
Pas d’échantilonnage \Delta t : intervalle de temps entre 2 prises de valeur
IMPORTANT [à retenir] : \boxed{\Delta t = 1/F_e} \boxed{F_e = 1/\Delta t}
Si on note t_n les valeurs discrètes du temps, alors : \Delta t = t_{n+1}-t_n
Les autres paramètres à considérer sont principalement :
Le nombre de points enregistrés: N_{pts}
La durée de l’enregistrement en secondes : \boxed{T_{enr} = N_{pts} \Delta t = N_{pts} / F_e}
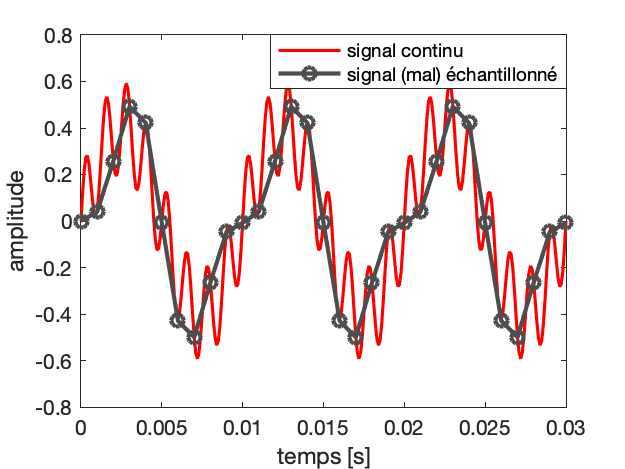
On s’aperçoit sur l’exemple de la figure suivante que la fréquence d’échantillonnage doit être nettement plus élevée que les fréquences des phénomènes que l’on analyse, sinon on ne pourra pas caractériser correctement des signaux altenatifs. Ici l’oscillation rapide n’est pas observable sur le signal numérisé :
EN PRATIQUE - [IMPORTANT à retenir !!!]
Retenir que la fréquence d’échantillonnage doit être > 2\times la fréquence maximum que l’on souhaite enregistrer :
\boxed{ F_e > 2 F_{max} }
ce qui s’exprime aussi sous cette forme :
\boxed{ F_{max} < F_e / 2 }
C’est le critère de Shannon
Remarques :
Pour s’assurer que ce critère est bien respecté, les appareils de bonne qualité commencent par appliquer un filtrage passe-bas pour supprimer les fréquences supérieures à F_e / 2 avant d’échantillonner le signal à la fréquencce F_e. Ce type de filtre est appelé filtre anti-repliement (ou anti aliasing filter en anglais). Voir la partie sur l’analyse fréquentielle.
Très souvent (mais pas systématiquement), pour assurer le respect du critère de Shannon, les cartes d’acquisition appliquent ce critère : F_{max} = F_e / 2,56 Ce sera le cas des boitiers d’acquisition utilisées en TP.
Noter que les oscilloscope numériques utilisés en TP n’ont pas de filtre anti-repliement et le critère de Shannon n’est pas forcément respecté. Voir démonstration en TP.
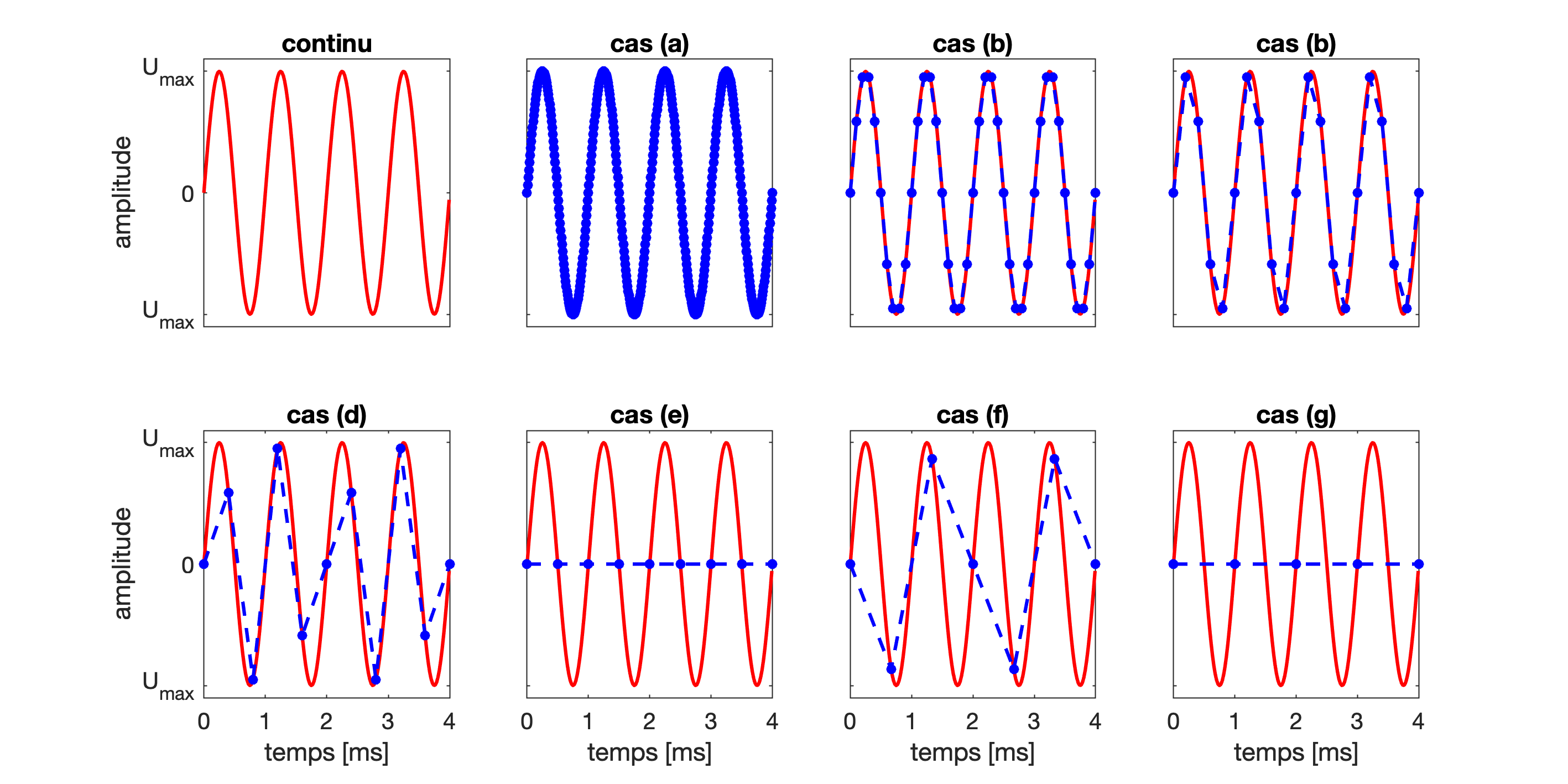
Exemple d’un signal échantillonné à différentes F_e
Exercice :
On numérise un signal de tension généré par un microphone au format .wav (signal audio) à la fréquence F_e=44100 Hz pendant 10 secondes.
Questions :
- Peut-on enregistrer des sons jusqu’à 20 000 Hz ?
- Combien d’échantillons (points sur la courbe) a-t-on enregistré ?
- Avec la même fréquencce d’échantillonnage, on enregistre 4096 points. Quelle est la durée de l’enregistrement ?
Réponses :
Si la fréquence maximum est F_{max} = 20000 Hz, et F_e = 44100 Hz, alors le critère de Shannon est bien respecté car F_e > 2 F_{max}, donc on conclut que ce réglage permet de numériser corrrectement des fréquences jusqu’à 20000 Hz.
D’après les relations précédentes, on déduit le nombre de points : N_{pts} = T_{enr} \times F_e = 10 \times 44100 = 441000
D’après les relations précédentes, on déduit T_{enr} = N_{pts} / F_e = 4096 / 44100 = 0,0929 \rm{s} = 92,9 \rm{ms}