1 Numérisation d’un signal (introduction)

Lors de l’acquisition numérique du signal par une carte d’acquisition (ou carte son, appareil de mesure, oscilloscope, …) dotée d’un convertisseur analogique-numérique, le signal analogique à variation continue est réduit à un ensemble de valeurs numériques caractérisant l’amplitude du signal prelevée à des instants successifs, généralement à intervalles réguliers.

Pour cela, plusieurs opérations sont réalisées :

1. l’échantillonnage prélève, le plus souvent à intervalles réguliers, la valeur du signal ;
   

2. la quantification transforme une valeur quelconque en une valeur prise dans une liste finie de valeurs valides pour le système ;
   

3. le codage fait correspondre à chaque valeur valide pour le système un code numérique.

   • La période d’échantillonnage à laquelle les valeurs du signal sont prélevées est fixée par le choix de la fréquence d’échantillonnage [eng: sampling frequency ou sampling rate].

   • La quantification permet d’approcher par un ensemble de valeurs discrètes l’amplitude d’un signal continu.

Remarques

• Plusieurs méthodes sont utilisées. [lien wikipedia]
• On se limite dans la suite à la quantification scalaire uniforme.
  
• On discutera essentiellement de la quantification des signaux temporels (1D) , mais c’est une opération également indispensable à la numérisation des images (2D) .

---

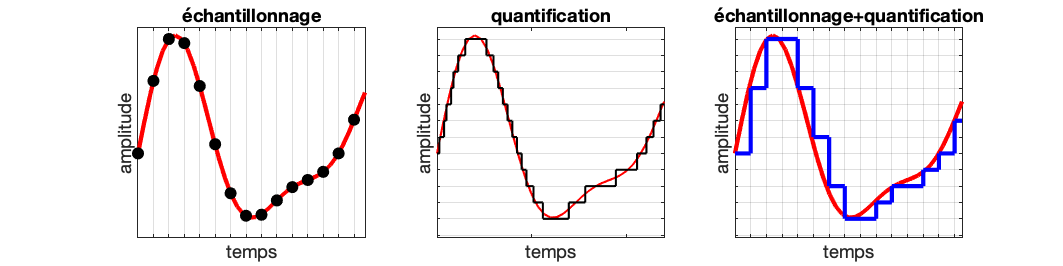
Légende:

• trait rouge: signal analogique s(t)
  
• à gauche : échantillonnage à intervalles réguliers. Points noirs : valeurs du signal écchantillonnées à des instants distants de \Delta t = 1/ F_e, avec F_e la fréquence d’échantillonnage.
  
• au milieu : on approche les valeurs continues du signal analogique par des valeurs prédéfines par le système d’acquisition et son réglage \longrightarrow trait noir
  
• à droite : en bleu, le résultat de la combinaison des deux opérations (signal bleu: rendu sous forme d’échantillonnage-blocage [wikipedia])

---

1.1 Erreurs dues à la numérisation

• L’erreur de quantification apparait lorsqu’il y a une conversion analogique-numérique du signal

• Les valeurs sont échantillonnées à intervalle de temps (le plus souvent régulier), déterminé par la fréquence d’échantillonnnage.

• L’amplitude d’un signal analogique s(t) est codée selon des valeurs numériques discrètes dont le pas \Delta s dépend du nombre de bits sur lequel l’amplitude est codée (codage sur 8 bits : 2^8 = 256 valeurs possibles, codage sur 12 bits : 2^{12} = 4096 valeurs possibles).

Par exemple : pour une carte d’acquisition dont le calibre d’entrée est \pm 10 Volts, le pas de quantification pour un codage sur 8 bits est 78.4 mV \left([10-(-10)]/2^8 = 78.4 \ 10^{-3}\right) tandis qu’il est de 4.88 mV \left([10-(-10)]/2^{12} = 4.88 \ 10^{-3}\right) pour un codage sur 12 bits (0.305 mV pour 16 bits, et 1.19 \muV pour 24 bits).

• L’incertitude maximale liée à la quantification d’un signal s(t) est de \pm\Delta s.

---

1.2 L’erreur de quantification dépend des paramètres de numérisation

Dans l’exemple ci-dessous on modifie les valeurs de la fréquence d’échantillonnage et du pas de quantification pour observer leur influence.

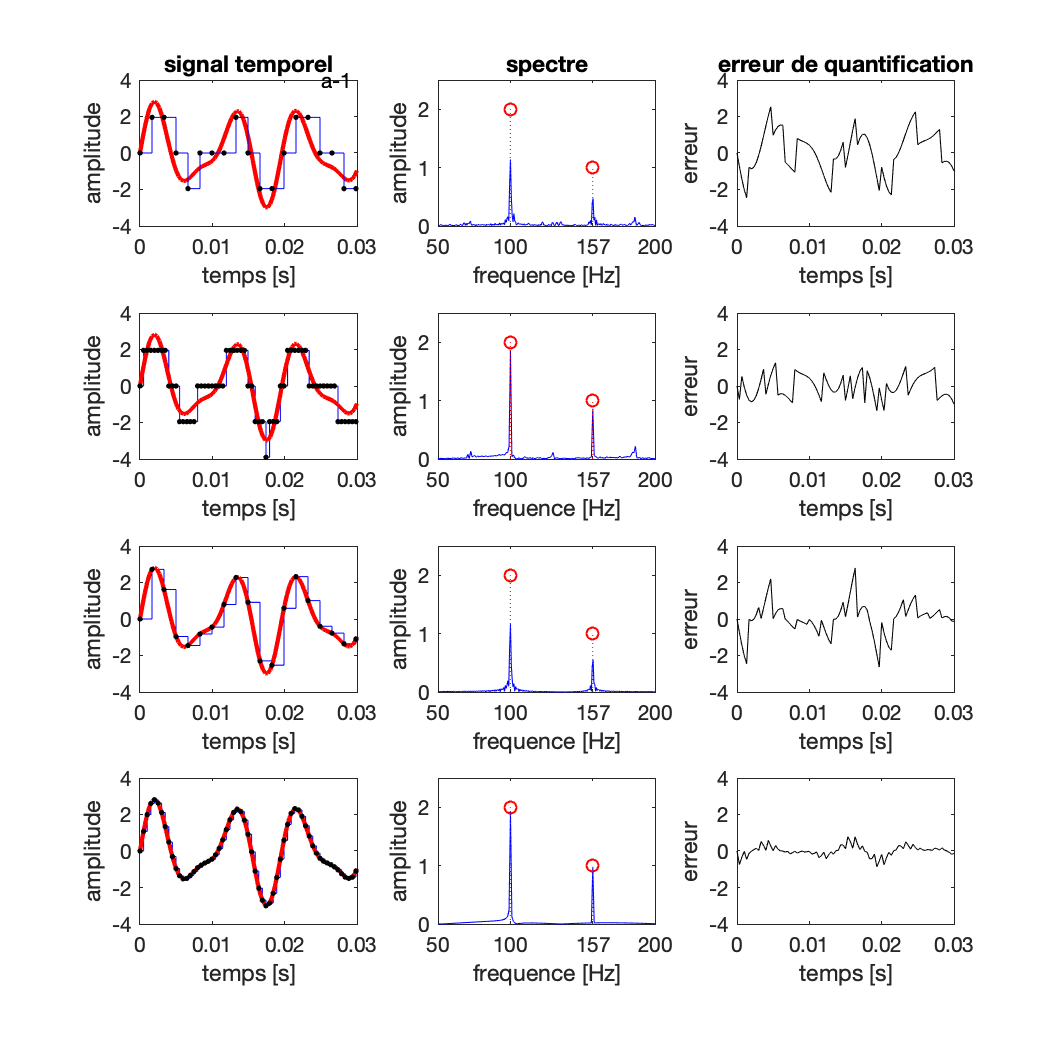
Légende :

Acquisition numérique et analyse spectrale d’un signal constitué de deux composantes sinusoidales :

s(t)= A_1 \sin (2 \pi F_1 t) + A_2 \sin (2 \pi F_2 t)
avec A_1=2, A_2=1, F_1=100 Hz, et F_2=157 Hz

• Figures :

  • gauche : signal temporel
  • milieu: spectre (analyse fréquentielle)
  • droite: erreur de quantification = différence numérisé - analogique

• de haut en bas : différents paramètres de numérisation : \Delta s et Fréquence d’échantillonnage F_e (et \Delta t).

  • ligne 1 : F_e = 603 Hz (\Delta t = 1.66 ms), \Delta s = 1.9531 Volts
    
  • ligne 2 : F_e = 2010 Hz (\Delta t = 0.50 ms), \Delta s = 1.9531 Volts
    
  • ligne 3 : F_e = 603 Hz (\Delta t = 1.66 ms), \Delta s = 0.0234 Volts
    
  • ligne 3 : F_e = 2010 Hz (\Delta t = 0.50 ms), \Delta s = 0.0234 Volts

• couleurs et symboles :

  • trait rouge : signal analogique (temporel s(t) et fréquentiel S(f) calculé par FFT)
  • trait bleu : signal numérisé (temporel s_n(t) et fréquentiel S_n(f)) - (restitution numérique \longrightarrow analogique sous la forme du blocage des valeurs).
  • trait noir : différence numérique - analogique s_n(t)-s(t)
    
  • points noirs : points mémorisés s_i
  • cerle rouge : amplitude réelle des deux composantes sinusoïdales

Commentaires :

• On constate que plus la fréquence d’échantillonnage est élevée et plus le pas de quantification est faible, plus le signal numérisé est proche du signal analogique
• L’erreur signal numérisé - signal analogique est alors d’autant plus réduite
• Pour minimiser l’erreur due à la quantification, il faut ajuster le niveau d’entrée de la carte d’acquisition au niveau de la source (jouer sur le calibre d’entrée, et/ou sur le gain d’amplification en amont de l’acquisition)
• En augmentant F_e (et donc en diminuant \Delta t), on améliore la description temporelle, au prix d’une augmentation du nombre de valeurs à mémoriser
• Plus la fréquence d’échantillonnage est élevée, et plus l’amplitude du signal est proche de la dynamique de l’échantillonneur, car on augmente la densité de points prélevée (pas d’échantillonnage \Delta t = 1/F_e.), et donc le signal numérisé ressemble le plus au signal analogique. En contrepartie, la taille mémoire, et les performances matérielles nécessaires pour le traitement rapide du signal augmentent (et donc aussi le prix et le coût énergétique).

---