10 Résolution fréquentielle

• La numérisation du signal implique l’analyse par transformation de Fourier discrète (TFD), et engendre également un spectre discret, connu seulement à des fréquences f_n = n \Delta f, où \Delta f est la résolution fréquentielle.

• Lorsque l’on calule le spectre avec un algorithme FFT (Fast Fourier Transform), en fixant un nombre de points N_{FFT}, la résolution fréquentielle est \Delta f = F_e/N_{FFT}. A noter: N_{FFT} peut être égal ou non au nombre d’échantillons enregistrés dans le domaine temporel. Souvent N_{FFT} est une puissance de 2 (512, 1024, 2048, ….etc).

• Lorsque l’on utilise un logiciel, ou un appareil (analyseur de spectre, oscilloscope numérique, collecteur de données, …), le nombre de points que l’on règle est généralement le nombre de points qui sera affiché, et pas le nombre de points utilisés pour le calcul. Le nombre de points affiché concerne une plage de fréquence inférieure à N_{FFT}/2. Par exemple, dans le cas d’un spectre calculé sur N_{FFT}=1024 points, si un appareil affiche le spectre dans l’intervalle [0, Fe/2.56], il s’affichera sur 1024/2.56 = 400 points. Ce nombre de points affichés est parfois appelé nombre de lignes dans certains logiciels ou appareils de mesure (ce sera le cas des appareils utilisés en TP de capteurs et vibrations).

• Le fait de discrétiser l’axe des fréquences a pour conséquence que l’on ne peut pas détecter des évolutions du spectre sur des intervalles de fréquence très étroits.

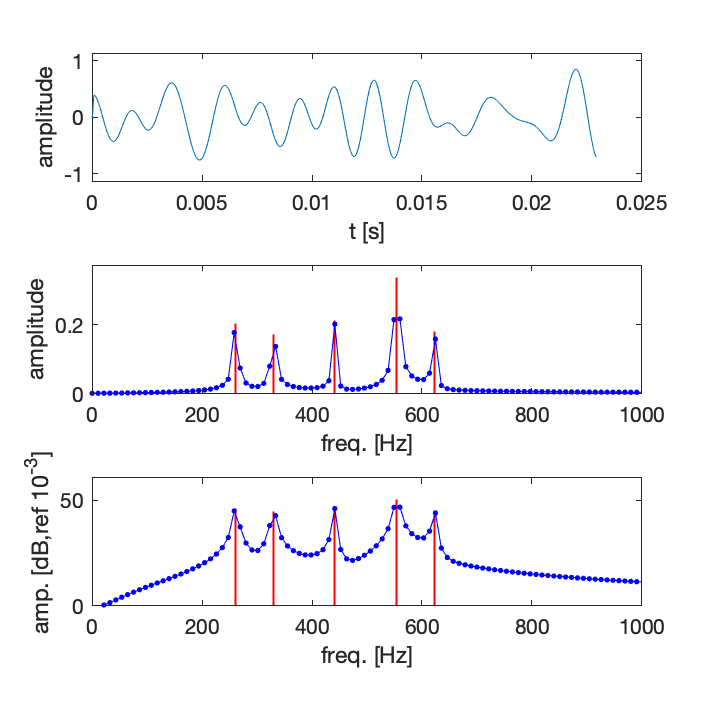
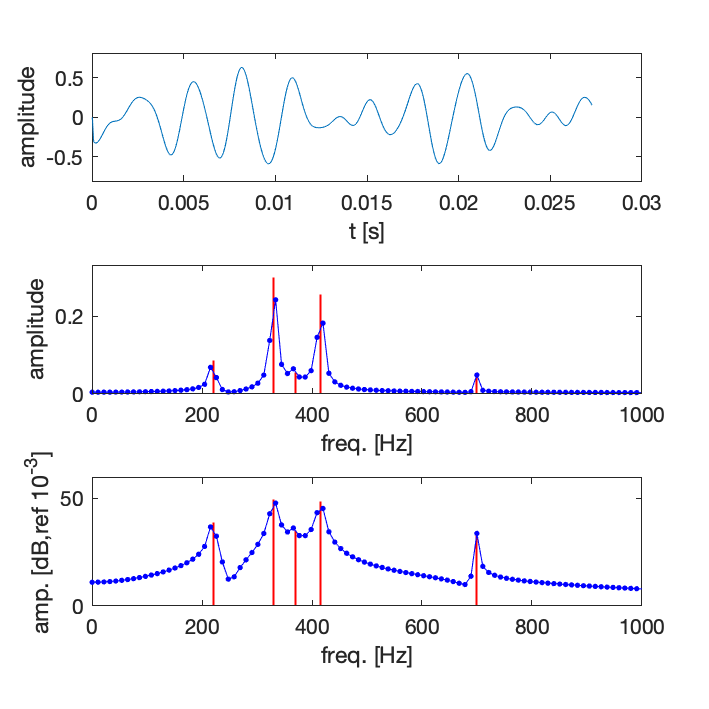
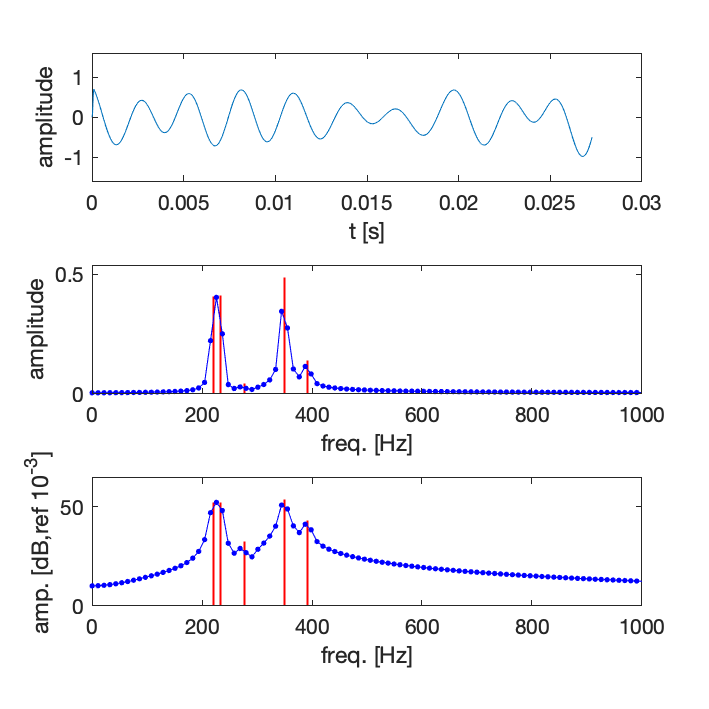
  On considère en général qu’il n’est possible de bien distinguer deux pics d’amplitude que s’ils sont séparés d’au moins 8 points.

  Cette limite peut être une base pour déterminer le nombre de points nécessaires, ou la fréquence d’échantillonnage si le nombre de points est fixé. Si la résolution fréquentielle est insufisante, alors on ne sera pas capable de distinguer les différentes composantes fréquentielles.

Exemples de spectres discrets obtenus par FFT

• F_e = 44100 Hz, N_{FFT} = 4096, \Delta f = 10.8 Hz
• Spectre obtenu par analyse FFT en bleu, spectre exact en rouge (5 fréquences)